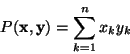

Esistono grandezze fisiche che per essere indicate richiedono unicamente
un valore numerico. Queste quantitá sono dette scalari (temperatura,
massa, ecc) e non presentano particolari difficoltá nella loro comprensione.
Ci sono peró anche grandezze, chiamate vettori, che vengono indicate
fornendo informazioni relative alla loro direzione e verso (forze,
accelerazioni ...). Geometricamente un vettore é rappresentabile con una
freccia caratterizzata dunque da una direzione, da un verso e da un punto
d'applicazione. Se non viene specificato il punto di applicazione si parla di
vettore libero.
- Due vettori
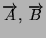 sono uguali solo se
hanno la stessa ampiezza o modulo, la stessa direzione e lo stesso verso.
sono uguali solo se
hanno la stessa ampiezza o modulo, la stessa direzione e lo stesso verso.
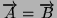
- Sia
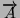 , allora il vettore avente lo stesso modulo e
direzione, ma verso opposto, viene indicato con
, allora il vettore avente lo stesso modulo e
direzione, ma verso opposto, viene indicato con
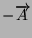 .
.
- La somma algebrica di due vettori
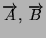 si ottiene applicando la
regola del parallelogramma. Da notare che la differenza tra due vettori
si ottiene applicando la
regola del parallelogramma. Da notare che la differenza tra due vettori
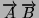 é pari alla somma di
é pari alla somma di
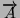 e
e
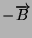 per quanto detto nel punto precedente.
per quanto detto nel punto precedente.
- Il prodotto di un vettore
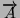 per un scalare h é ancora un vettore,
per un scalare h é ancora un vettore,
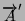 , avente la stessa direzione ma modulo pari a
, avente la stessa direzione ma modulo pari a
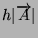 . Se h é negativo allora il
verso di
. Se h é negativo allora il
verso di
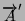 é opposto a quello di
é opposto a quello di
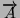 .
.
- Le grandezze fisiche vettoriali appartengono a quello che in geometria
viene definito uno spazio vettoriale su campo reale. Per
comoditá riportiamo qui di seguito la definizione generale di spazio
vettoriale: Siano l'insieme R dei numeri reali e
V un insieme. Si dice che V é uno spazio vettoriale se:
- É definita in V una somma ovvero un'operazione che associa ad
ogni coppia (a,b) di elementi di V un unico elemento di V indicato
con a+b.
- É definito un prodotto esterno con elementi di R, ovvero
un'operazione che associa alla coppia di elementi (a,h) con a
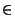 V e h
V e h 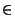 R, un elemento
R, un elemento 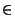 V
chiamato ah.
V
chiamato ah.
- Le due operazioni definite debbono soddisfare alcune regole:
- a)
- SOMMA: Proprietá associativa, proprietá commutativa, esistenza
dell'elemento neutro, esistenza dell'opposto, proprietá distributiva.
- b)
- PRODOTTO ESTERNO: Esistenza del neutro, proprietá associativa e
distributiva.
A questa definizione é necessario aggiungere il concetto di prodotto
scalare: Sia V uno spazio vettoriale su campo reale. Definisco
prodotto scalare quella applicazione
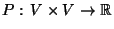 (attenzione quindi che il p.s.
é uno scalare) con le seguenti proprietá:
(attenzione quindi che il p.s.
é uno scalare) con le seguenti proprietá:
- a)
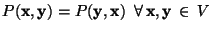
-
- b)
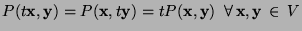 ,
,
-
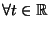
- c)
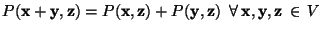
-
- d)
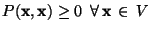
- e pari a 0 solo se x=0.
In
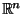 un prodotto scalare che puó essere definito é:
un prodotto scalare che puó essere definito é:
a cui é associata naturalmente la norma:
Il prodotto scalare che abbiamo definito non é l'unico possibile, ma é quello
che viene adottato normalmente, pertanto ci atterremo a questo.
Un'altra operazione fortemente utilizzata é il prodotto vettoriale
e nasce dal concetto fisico di momento di una forza.
Il prodotto vettoriale dá come risultato un vettore (c) che ha
per modulo il prodotto
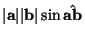 . Si
noti che se i due vettori sono collineari allora il prodotto é nullo. La
direzione é quella ortogonale al piano individuato dai due vettori a e
b mentre il verso si determina applicando la regola della mano destra.
É evidente che scambiando l'ordine dei due vettori il prodotto cambia solo
nel verso, si dice cioé che é anticommutativo.
. Si
noti che se i due vettori sono collineari allora il prodotto é nullo. La
direzione é quella ortogonale al piano individuato dai due vettori a e
b mentre il verso si determina applicando la regola della mano destra.
É evidente che scambiando l'ordine dei due vettori il prodotto cambia solo
nel verso, si dice cioé che é anticommutativo.
Un particolare da tenere bene in mente é che i versori della comune terna
di assi i,j,k ortogonali soddisfano la seguente
relazione ¨circolare¨:
 |
(1) |
Si puó pure dimostrare che il prodotto vettoriale é distributivo sia a destra
che a sinistra, cioé:
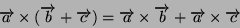 |
(2) |
e
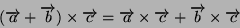 |
(3) |
Applicando le eq.1, 2, 3
si ricava che il prodotto vettoriale vale, in coordinate cartesiane:
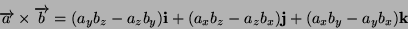 |
(4) |
Quest'ultima equazione puó essere comodamente riscritta in notazione
matriciale ricordando la definizione di determinante:
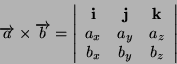 |
(5) |
Infine esiste il prodotto misto, operazione in cui compare sia il
prodotto scalare che quello vettoriale:
É possibile inoltre definire anche le operazioni matematiche di derivazione e
d'integrazione. Per la derivazione vettoriale vale il concetto di
limite del rapporto incrementale rispetto ad un parametro u:
purché tale limite esista. Se il vettore F(u) é scomponibile in
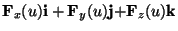 o piú in generale in una qualunque base vettoriale, allora
o piú in generale in una qualunque base vettoriale, allora
Inoltre le consuete regole e proprietá della operazione di derivazione
sono mutuate dall´analisi:
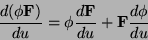 |
(6) |
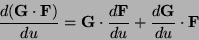 |
(7) |
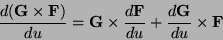 |
(8) |
Per quanto riguarda invece l'operazione d'integrazione si puó dire che dato
un vettore
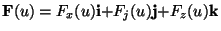 ,
posso definire in generale:
,
posso definire in generale:
This document was generated using the LaTeX2HTML
translator Version 2002 (1.62)
Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer
Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics
Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -no_subdir -split 0 -show_section_numbers
/tmp/lyx_tmpdir9893U9NR3c/lyx_tmpbuf0/introa.tex
The translation was initiated by root on 2004-01-08


root 2004-01-08