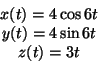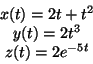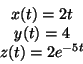1 Esercizi di Cinematica

La traiettoria di un punto nello spazio tridimensionale é espressa con:

$\begin{displaymath} \begin{array}{c} x(t)=4\cos6t\\ y(t)=4\sin6t\\ z(t)=3t\end{array}\end{displaymath}$

calcolare la lunghezza d'arco percorsa dal punto in movimento dopo un tempo 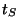$t_{S}$ =5s.
Un punto si muove nello spazio con equazioni parametriche:

$\begin{displaymath} \begin{array}{c} x(t)=2t+tÂ²\\ y(t)=2tÂ³\\ z(t)=2e^{-5t}\end{array}\end{displaymath}$

calcolare la velocitá e l'accelerazione in coordinate cartesiane in ogni istante. In particolare calcolare il modulo della velocitá iniziale del punto.
L'accelerazione di una particella vale

$\begin{displaymath} \overrightarrow{a}=5e^{-3t}\mathbf{i}+4\sin5t\mathbf{j}-2\cos t\mathbf{k}\end{displaymath}$

calcolare il valore della velocitá vettoriale in funzione del tempo sapendo che per t=0 la velocitá assume il valore:

$\begin{displaymath} \overrightarrow{v}=-\mathbf{i}-\mathbf{j}+\mathbf{k}\end{displaymath}$

Infine determinare l'espressione del vettore posizione sapendo che all'istante t=0 il punto si trova in P(2,1,2).
Due punti hanno vettori posizione rispettivamente pari a

$\begin{displaymath} \begin{array}{c} \overrightarrow{r_{1}}=t\mathbf{i}+3tÂ²\math... ...row{r_{2}}=6t\mathbf{i}+(3tÂ²+7)\mathbf{j}+\mathbf{k}\end{array}\end{displaymath}$

determinare i valori della velocitá relativa e dell'accelerazione relativa.
Dato il vettore posizione

$\begin{displaymath} \overrightarrow{r}=3\cos3t\mathbf{i}+3\sin3t\mathbf{j}+(5t+2)\mathbf{k}\end{displaymath}$

calcolare i vettori tangente, normale e binormale. Verificare infine che la velocitá é effettivamente esprimibile come:

$\begin{displaymath} \overrightarrow{v}=\left\vert v\right\vert\hat{T}\end{displaymath}$
Dell'esercizio precedente calcolare il raggio di curvatura relativo al cerchio osculatore.
Il vettore posizione di una particella data é

$\begin{displaymath} \overrightarrow{r}=3\mathbf{i}\sin\omega t+3\mathbf{j}\cos\omega t\end{displaymath}$

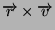dimostrare che la velocitá del punto é perpendicolare ad $\overrightarrow{r}$ e calcolare l'accelerazione. Mostrare infine che il prodotto vettoriale $\overrightarrow{r}\times\overrightarrow{v}$ é una costante del moto.
Il vettore posizione di una particella che si muove su di una traiettoria ellittica é

$\begin{displaymath} \overrightarrow{r}=a\mathbf{i}\sin\omega t+b\mathbf{j}\cos\omega t\end{displaymath}$

determinare la velocitá e l'accelerazione.
Un traghettatore fluviale deve portare un cliente da una riva all'altra del fiume che é largo D=50m. La corrente ha una velocitá, in modulo, pari a V=1m/s ed il molo di attracco si trova esattamente di fronte a quello di partenza. Sapendo che la velocitá, in modulo, della barca vale v=3m/s spiegare in che modo il traghettatore deve muoversi per raggiungere esattamente la sponda opposta nel punto di attracco. Indicare pure il tempo di attraversamento.
Una scimmia cammina per 65 m alla velocitá di 3Km/h sempre nella stessa direzione lungo un binario della ferrovia. Poi inizia a correre trascinandosi per circa 2 minuti seguendo la direzione precedente. Calcolare la velocitá media totale.
La velocitá media é un vettore. Data la legge oraria in forma cartesiana:

$\begin{displaymath} \begin{array}{c} x(t)=2t\\ y(t)=4\\ z(t)=2e^{-5t}\end{array}\end{displaymath}$

calcolare la velocitá media relativa ad un tempo compreso tra t=0s e t=3s.
Un treno parte da Faenza e raggiunge Bologna dopo un tempo di 33 minuti. Il percorso compiuto é di circa 50 Km. Calcolare la velocitá media di questo tratto. Infine determinare la velocitá media totale se il treno appena arrivato a Bologna ritorna immediatamente a Faenza impiegando un tempo di 45 minuti. Qual é la velocitá del treno nell'istante t=10 minuti?
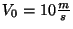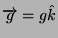Un bambino si trova al primo piano di un condominio ed ha in mano un sasso. Il bambino decide di lanciare il sasso e gli imprime una velocitá $V_{0}=10\frac{m}{s}$ e la sua traiettoria, inizialmente forma con l'orizzontale un angolo di 60 gradi. Considerare l'altezza di partenza del sasso pari a 5m dal suolo. Ricavare l'equazione del moto sapendo che l'unica accelerazione in gioco é la gravitá $\overrightarrow{g}=-g\hat{k}$ . (g=9.81 $\frac{m}{sÃÂ²}$ )
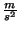L'equazione della traiettoria si ottiene esprimendo la coordinata z come funzione della variabile distanza y eliminando la dipendenza esplicita dal tempo. Ricavare dunque la traiettoria del moto descritto nel punto precedente.
Due fucili sparano in versi opposti lungo la direzione y di un sistema di riferimento Oxyz ortogonale. Entrambi i fucili sono posizionati nel punto A(x',0,h). La velocitá del proiettile all'uscita della canna del secondo fucile é pari, in modulo, al doppio della velocitá raggiungibile dal proiettile esploso dal primo fucile. Calcolare i due tempi di caduta e le due gittate sapendo che nella regione considerata vale l'accelerazione di gravitá.
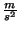Un'automobile si muove di moto rettilineo uniforme lungo una strada di campagna alla velocitá di $V_{0}=70\frac{Km}{h}$ . All'improvviso un capriolo attraversa la strada ad una distanza iniziale d=30m. Se l'auto inchioda imprimendo un'accelerazione negativa di -5 $\frac{m}{sÃÂ²}$ , l'automobilista riuscirá a non travolgere il povero animale?
Un razzo sperimentale della Nasa viene lanciato verticalmente e sale con un'accelerazione costante pari a 30. La spinta cessa dopo un minuto quando tutto il combustibile é terminato. Qual é la massima altezza raggiunta? Quanto tempo impiega a raggiungerla?