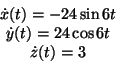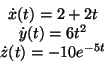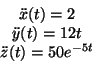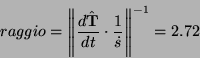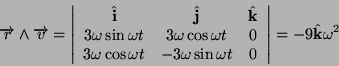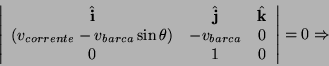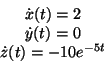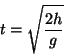- Per prima cosa bisogna determinare la velocità con la quale il punto
si muove:
questa è una velocità vettoriale perciò posso trovarne il modulo:
e rappresenta proprio la velocità con la quale il punto si sulla traiettoria.
Pertanto la distanza percorsa vale semplicemente:
dove la quantità s è proprio l'ascissa curvilinea.
- Anche in questo esercizio si può calcolare molto semplicemente le
componenti della velocità come:
mentre per trovare l'accelerazione occorre derivare una seconda volta:
All' istante t=0 il modulo della velocità vale:
- Qui si tratta di applicare l'operazione inversa:
Ovviamente esistono infinite primitive che soddisfano l'equazione
sopra citata. Per questo motivo, per determinare l'integrale esatto,
è necessario avere un'ulteriore informazione. In questo caso il dato
aggiuntivo è la velocità del punto all'istante t=0.
All'istante t=0 si ha che
segue che
in definitiva
Infine se voglio calcolare il vettore posizione debbo iterare nuovamente
la procedura:
impongo la posizione al tempo t=0:
Perciò:
- Calcoliamo il vettore
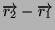 .
La sua derivata fornisce esattamente il valore della velocità. Segue
alla stessa maniera l'accelerazione:
.
La sua derivata fornisce esattamente il valore della velocità. Segue
alla stessa maniera l'accelerazione:
- Come prima cosa calcoliamo il vettore velocità istantanea:
il cui modulo vale:
Posso calcolare il versore tangente alla curva:
Se calcolo la derivata del versore rispetto al tempo ottengo:
ma
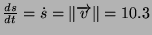 ,
indi per cui:
,
indi per cui:
il modulo dell'ultimo vettore fornisce proprio il versore
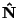 :
:
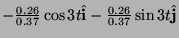 .
Il prodotto vettoriale tra i versori
.
Il prodotto vettoriale tra i versori
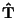 e
e
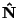 regala infine il terzo versore
regala infine il terzo versore
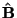 .
.
- Riprendiamo i risultati del precedente esercizio. Il vettore
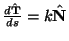 esprime la relazione che andiamo ad utilizzare per ricavare il valore
del raggio di curvatura r. Infatti la costante k=1/r. Segue che il
raggio di curvatura vale
esprime la relazione che andiamo ad utilizzare per ricavare il valore
del raggio di curvatura r. Infatti la costante k=1/r. Segue che il
raggio di curvatura vale
- Calcoliamo immediatamente il valore della velocità vettoriale istantanea:
quindi l'accelerazione vale
Per vedere che il vettore posizione è perpendicolare alla velocità
basta fare il prodotto scalare tra i due vettori:
Calcoliamo infine il prodotto vettore
è evidente il fatto che questo valore non dipende dal tempo.
- Anche questo esercizio si risolve in maniera analoga. L'unica cosa
che cambia la forma della traiettoria. La velocità:
quindi l'accelerazione vale
il cui modulo vale
- Si tratta di considerare il moto della barca come frutto della composizione
di due velocità. Se chiamamo
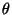 l'angolo compreso tra la direzione
della barca e la retta congiungente il punto di partenza e quello
di partenza, allora otteniemo che
l'angolo compreso tra la direzione
della barca e la retta congiungente il punto di partenza e quello
di partenza, allora otteniemo che
quindi bisogna imporre che la velocità vettoriale somma sia collineare
alla retta congiungente i due punti di attracco. Se usiamo il sistema
di riferimento implicito che associa alla direzione della corrente
il versore
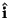 e alla direzione della retta il versore
e alla direzione della retta il versore
 , allora significa che:
, allora significa che:
Lo spostamento della barca avviene in direzione perpendicolare alla
corrente del fiume, pertanto per determinare il tempo impiegato per
l'attraversamento è necessario conoscere il modulo della velocità
del sistema barca+corrente (non è l'unico modo):
segue che il tempo totale è:
- La definizione di velocità media coinvolge il tempo totale e lo spazio
totale, cioè:
bisogna notare che in generale
pertanto
- E' conveniente trovare la velocità in forma cartesiana:
cioè
Questa velocità è quella istantanea che è diversa da quella media.
Lo spostamento totale realizzato tra t=0 e t=3s si ottiene:
per cui la velocità media vettoriale vale:
- Il primo punto è decisamente banale pertanto tralascio la soluzione.
Il secondo quesito prevede che si ragioni in termini vettoriali la
velocità media totale è nulla perchè lo spostamento totale
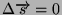 poichè il treno ritorna al punto di partenza. Infine, per l'ultimo
punto possiamo dire che non conosciamo la legge oraria che governa
il treno, pertanto non possiamo dire nulla su una velocità istantanea.
poichè il treno ritorna al punto di partenza. Infine, per l'ultimo
punto possiamo dire che non conosciamo la legge oraria che governa
il treno, pertanto non possiamo dire nulla su una velocità istantanea.
- Nel sistema in questione agisce solamente l'accelerazione di gravità
che è diretta verso il basso. Consideriamo un sistema di riferimento
con l'asse delle ordinate diretto verso il basso e l'asse delle ascisse
orientato lungo nel ''verso positivo'' del moto. Il sasso parte
dalle coordinate (0,-5) per cui le equazioni del moto si ricavano
partendo da
segue che
L'idea di realizzare integrazioni successive è un modo efficace per
pervenire alla soluzione. Le due costanti si determinano grazie alle
condizioni iniziali della velocità:
e dunque:
- Ricaviamo t in funzione di x:
da cui
- Il fatto che i fucili siano orientati paralleli all'asse delle ascisse
semplifica i calcoli. Anche in questo caso l'unica forza che agisce
concretamente è la forza di gravità. Le pallottole, una volta sparate,
hanno velocità che hanno la componente lungo x costante mentre l'unica
che cambia è la componente verticale con la legge di un moto uniformemente
accelerato. Pertanto la caduta delle due pallottole termina nello
stesso istante, ma con punti di caduta diversi. La figura 1
mostra proprio che una pallina lasciata cadere semplicemente ed una
dotata di velocità lungo x, si muovono sulla verticale nello stesso
modo. Il tempo di caduta è:
mentre le gittate sono, in modulo una il doppio dell'altra.
Figure 1:
Foto stroboscopica con tempo di intervallo 1/30
|
|
This document was generated using the
LaTeX2HTML translator Version 2002 (1.62)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -no_subdir -split 0 -show_section_numbers /tmp/lyx_tmpdir4109Mst0kg/lyx_tmpbuf1/soluz2.tex
The translation was initiated by gabriele on 2004-02-07



gabriele
2004-02-07