Università di Bologna - Facoltà di
Ingegneria II - Sede di Forlì
|
 |
Fisica Generale Interattiva
prof. Domenico Galli
|
|
 Caduta di una sfera
in un fluido viscoso (resistenza parametrizzata in funzione di CD)
Caduta di una sfera
in un fluido viscoso (resistenza parametrizzata in funzione di CD)
Punto materiale sferico soggetto alla forza peso, alla
forza idrostatica e
alla forza resistente esercitata dal fluido (parametrizzata in funzione
di CD)
Soluzione mediante il metodo di Runge-Kutta del IV
ordine
La forza agente sul punto materiale è:
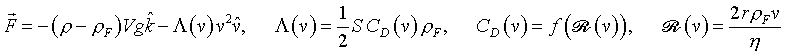
dove 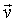 è la velocità della sfera, r è il
suo raggio,
è la velocità della sfera, r è il
suo raggio, 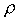 la sua
densità, V il suo volume e S la sua sezione (ovvero
l'area del suo cerchio massimo);
la sua
densità, V il suo volume e S la sua sezione (ovvero
l'area del suo cerchio massimo);
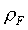 è la densità
del fluido,
è la densità
del fluido, 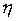 la sua viscosità;
la sua viscosità; 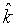 è il versore verticale ascendente e g è l'accelerazione
di gravità; CD è il
coefficiente (adimensionale) di smorzamento.
è il versore verticale ascendente e g è l'accelerazione
di gravità; CD è il
coefficiente (adimensionale) di smorzamento.
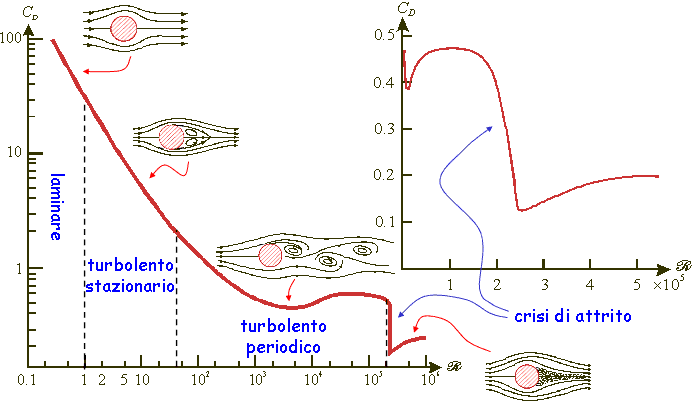
Il coefficiente CD dipende
del numero di Reynolds 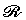 secondo la funzione empirica rappresentata nei grafici più sotto.
Prendendo l'asse z nella direzione di
secondo la funzione empirica rappresentata nei grafici più sotto.
Prendendo l'asse z nella direzione di
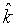 e scegliendo una velocità iniziale senza componenti orizzontali,
il moto avviene lungo l'asse z
(perché forza e velocità hanno la stessa direzione);
le equazioni del moto e le condizioni iniziali si scrivono:
e scegliendo una velocità iniziale senza componenti orizzontali,
il moto avviene lungo l'asse z
(perché forza e velocità hanno la stessa direzione);
le equazioni del moto e le condizioni iniziali si scrivono:
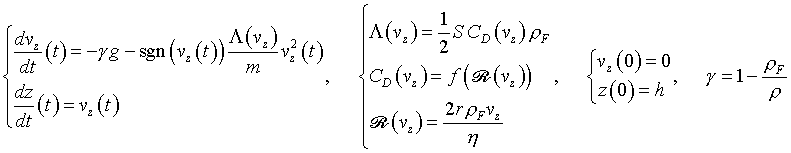
dove m è la massa della sfera.
Parametri e condizioni iniziali suggeriti per iniziare:
- Densità sfera = 1000 kg/m³, Raggio sfera = 0.001 m,
Densità fluido = 1.25 kg/m³, Viscosità fluido= 1.82
· 10-5 kg m-1 s-1, Altezza
iniziale = 0 m, Intervallo di tempo = 2 s, Intervallo di scansione =
0.02 s (gocciolina d'acqua che cade nell'aria).
- Densità sfera = 7860 kg/m³, Raggio sfera = 0.001 m,
Densità fluido = 963 kg/m³, Viscosità fluido =
1.11 kg m-1 s-1, Altezza iniziale = 0 m,
Intervallo di tempo = 0.007 s, Intervallo di scansione = 7 · 10-5
s (pallino di ferro che cade nell'olio di ricino, regime laminare).
- Densità sfera = 7860 kg/m³, Raggio sfera = 0.02 m,
Densità fluido = 1.25 kg/m³, Viscosità fluido = 1.82
· 10-5 kg m-1 s-1, Altezza
iniziale = 0 m, Intervallo di tempo = 20 s, Intervallo di scansione =
0.2 s (biglia di ferro che cade nell'aria).
Diminuendo l'intervallo si scansione migliora la precisione dei
risultati.
Per avviare l'Applet "cliccare" il bottone qui sotto.
Algoritmo di Runge-Kutta del IV
ordine per il punto materiale in caduta in un fluido viscoso, con
resistenza parametrizzata in funzione di CD:
for(i=0;t<tMax;)
{
// algoritmo di Runge-Kutta IV ordine
k1=v*deltaT;
j1=a*deltaT;
vm1=v+j1/2;
am1=-gamma*g-0.5*getCd(2*vm1*r*rof/eta)*rof*s*vm1*Math.abs(vm1)/m;
k2=vm1*deltaT;
j2=am1*deltaT;
vm2=v+j2/2;
am2=-gamma*g-0.5*getCd(2*vm2*r*rof/eta)*rof*s*vm2*Math.abs(vm2)/m;
k3=vm2*deltaT;
j3=am2*deltaT;
vf=v+j3;
af=-gamma*g-0.5*getCd(2*vf*r*rof/eta)*rof*s*vf*Math.abs(vf)/m;
k4=vf*deltaT;
j4=af*deltaT;
z=z+(k1+2*k2+2*k3+k4)/6;
v=v+(j1+2*j2+2*j3+j4)/6;
re=Math.abs(2*v*r*rof/eta); // numero di Reynolds
cd=getCd(re); // coefficiente di smorzamento
a=-gamma*g-0.5*cd*rof*s*v*Math.abs(v)/m;
// fine algoritmo di Runge-Kutta IV ordine
t=t+deltaT;
i++;
if(t>tMax)break;
// se ci sono > 10000 punti, memorizza 1 punto ogni storePeriod punti
if(i%storePeriod==0)
{
lzt.add(new Point2D.Float((float)t,(float)z));
lvt.add(new Point2D.Float((float)t,(float)v));
lat.add(new Point2D.Float((float)t,(float)a));
lrt.add(new Point2D.Float((float)t,(float)re));
lct.add(new Point2D.Float((float)t,(float)cd));
lvz.add(new Point2D.Float((float)z,(float)v));
}
}
Metodo utilizzato per la
parametrizzazione di CD in funzione del numero di Reynolds:
public double getCd(double re)
{
re=Math.abs(re);
if(re<Double.MIN_VALUE)return 0.; // velocita' 0 => forza 0
if(re<1)return 24.*Math.pow(re,-1);
else if(re<2)return 24.*Math.pow(re,-0.78);
else if(re<5)return 25.6*Math.pow(re,-0.87);
else if(re<10)return 18.25*Math.pow(re,-0.66);
else if(re<20)return 18.62*Math.pow(re,-0.67);
else if(re<50)return 16.57*Math.pow(re,-0.63);
else if(re<100)return 7.01*Math.pow(re,-0.41);
else if(re<200)return 10.6*Math.pow(re,-0.5);
else if(re<500)return 5.62*Math.pow(re,-0.38);
else if(re<2e3)return 2.36*Math.pow(re,-0.24);
else if(re<5e3)return 0.75*Math.pow(re,-0.09);
else if(re<5e4)return 3.04e-16*re*re*re-7.11e-11*re*re+5.56e-6*re+0.322;
else if(re<1.5e5)return -4.4e-12*re*re+9.4e-7*re+0.424;
else if(re<2.5e5)return -1.43e-16*re*re*re+5.12e-11*re*re-6.16e-6*re+0.721;
else if(re<5e5)return 0.005*Math.pow(re,0.274);
else return 0.024*Math.pow(re,0.152);
}
Densità e viscosità di alcuni
fluidi
|
|
densità [kg/m³] |
viscosità [kg m-1 s-1] |
| Aria a 0 °C |
1.25
|
1.82 ·
10-5
|
| Etere a 18 °C |
7.19 ·
102 |
2.38 ·
10-4 |
| Acqua a 0 °C |
1.00 ·
103
|
1.8 ·
10-3 |
| Acqua a 10 °C |
1.00 ·
103 |
1.3 ·
10-3 |
| Acqua a 20 °C |
1.00 ·
103 |
1.0 ·
10-3 |
| Acqua a 30 °C |
1.00 ·
103 |
8 · 10-4 |
| Acqua a 100 °C |
1.00 ·
103 |
2.8 ·
10-5 |
| Alcool a 18 °C |
8.18 ·
102
|
1.25 ·
10-3 |
| Mercurio a 18 °C |
1.3 ·
104
|
1.57 ·
10-2 |
| Olio di ricino a 18 °C |
9.63 ·
102
|
1.11
|
| Glicerina a 2.8 °C |
1.25 ·
103
|
4.22
|
| Glicerina a 18 °C |
1.25 ·
103 |
1.18
|
| Glicerina a 20 °C |
1.25 ·
103 |
0.83
|
| Glicerina a 26.5 °C |
1.25 ·
103 |
0.49
|
Densità di alcuni solidi
|
|
densità [kg/m³] |
Ghiaccio
|
9.17 ·
102
|
Magnesio
|
1.74 ·
103 |
Vetro
|
2.5 ·
103 |
Alluminio
|
2.70 ·
103 |
Zinco
|
7.12 ·
103 |
Stagno
|
7.28 ·
103 |
Ferro
|
7.86 ·
103 |
Ottone
|
8.5 ·
103 |
Bronzo
|
8.8 ·
103 |
Rame
|
8.9 ·
103 |
Argento
|
1.05 ·
104 |
Piombo
|
1.14 ·
104 |
Uranio
|
1.87 ·
104 |
Oro
|
1.94 ·
104 |
Platino
|
2.14 ·
104 |
 Indice Fisica Interattiva
Indice Fisica Interattiva
March 1, 2004, Domenico
Galli
