Università di Bologna - Facoltà di
Ingegneria II - Sede di Forlì
|
 |
Fisica Generale Interattiva
prof. Domenico Galli
|
|
 Traiettoria di un
proiettile sferico nell'aria
Traiettoria di un
proiettile sferico nell'aria
Punto materiale sferico con velocità
iniziale, soggetto alla forza peso e alla forza resistente esercitata
dal fluido (parametrizzata in funzione di CD)
Soluzione mediante il metodo di Runge-Kutta del IV
ordine
Parametri e condizioni iniziali suggeriti per iniziare:
- Densità sfera = 7860 kg/m³, Raggio sfera = 0.01 m,
Densità fluido = 1.25 kg/m³, Viscosità fluido = 1.82
· 10-5 kg m-1 s-1, Velocità
iniziale = 1000 m/s, Altezza iniziale = 0 m, Angolo di lancio =
23º, Intervallo di scansione = 0.04 s.
- Densità sfera = 7860 kg/m³, Raggio sfera = 0.01 m,
Densità fluido = 1.25 kg/m³, Viscosità fluido = 1.82
· 10-5 kg m-1 s-1, Velocità
iniziale = 1000 m/s, Altezza iniziale = 0 m, Angolo di lancio =
45º, Intervallo di scansione = 0.04 s.
- Densità sfera = 7860 kg/m³, Raggio sfera = 0.01 m,
Densità fluido = 1.25 kg/m³, Viscosità fluido = 1.82
· 10-5 kg m-1 s-1, Velocità
iniziale = 1 m/s, Altezza iniziale = 0 m, Angolo di lancio = 23º,
Intervallo di scansione = 0.00004 s.
- Densità sfera = 7860 kg/m³, Raggio sfera = 0.01 m,
Densità fluido = 1.25 kg/m³, Viscosità fluido = 1.82
· 10-5 kg m-1 s-1, Velocità
iniziale = 1 m/s, Altezza iniziale = 0 m, Angolo di lancio = 45º,
Intervallo di scansione = 0.00004 s.
Diminuendo l'intervallo si scansione migliora la precisione dei
risultati.
Si osservi che per piccole
velocità iniziali la traiettoria è simmetrica con
forma simile a una parabola e
si avvicina molto alla traiettoria nel vuoto, mentre per grandi velocità iniziali la
traiettoria è fortemente asimmetrica
e il primo tratto di essa è praticamente
rettilineo: il motivo è che nel primo tratto, la
resistenza (che ha la stessa direzione della velocità e dunque
non curva la traiettoria) è talmente intensa da rendere
praticamente trascurabile
l'effetto della forza di gravità
sulla somma vettoriale delle due forze.
Si osservi inoltre che l'angolo
corrispondente alla massima gittata, per piccole velocità
iniziali è pari a circa 45º, mentre per grandi
velocità iniziali è notevolmente più piccolo.
Per avviare l'Applet "cliccare" il bottone qui sotto.
Algoritmo di Runge-Kutta del IV
ordine per il proiettile sferico nell'aria, con resistenza
parametrizzata in funzione di CD:
for(i=0;z>=0;)
{
// algoritmo di Runge-Kutta IV ordine
kx1=vx*deltaT;
jx1=ax*deltaT;
vxm1=vx+jx1/2;
kz1=vz*deltaT;
jz1=az*deltaT;
vzm1=vz+jz1/2;
vm1=Math.sqrt(vxm1*vxm1+vzm1*vzm1);
axm1=-0.5*getCd(2*vm1*r*rof/eta)*rof*s*vxm1*vm1/m;
azm1=-gamma*g-0.5*getCd(2*vm1*r*rof/eta)*rof*s*vzm1*vm1/m;
kx2=vxm1*deltaT;
jx2=axm1*deltaT;
vxm2=vx+jx2/2;
kz2=vzm1*deltaT;
jz2=azm1*deltaT;
vzm2=vz+jz2/2;
vm2=Math.sqrt(vxm2*vxm2+vzm2*vzm2);
axm2=-0.5*getCd(2*vm2*r*rof/eta)*rof*s*vxm2*vm2/m;
azm2=-gamma*g-0.5*getCd(2*vm2*r*rof/eta)*rof*s*vzm2*vm2/m;
kx3=vxm2*deltaT;
jx3=axm2*deltaT;
vxf=vx+jx3;
kz3=vzm2*deltaT;
jz3=azm2*deltaT;
vzf=vz+jz3;
vf=Math.sqrt(vxf*vxf+vzf*vzf);
axf=-0.5*getCd(2*vf*r*rof/eta)*rof*s*vxf*vf/m;
azf=-gamma*g-0.5*getCd(2*vf*r*rof/eta)*rof*s*vzf*vf/m;
kx4=vxf*deltaT;
jx4=axf*deltaT;
x=x+(kx1+2*kx2+2*kx3+kx4)/6;
vx=vx+(jx1+2*jx2+2*jx3+jx4)/6;
kz4=vzf*deltaT;
jz4=azf*deltaT;
z=z+(kz1+2*kz2+2*kz3+kz4)/6;
vz=vz+(jz1+2*jz2+2*jz3+jz4)/6;
v=Math.sqrt(vx*vx+vz*vz);
re=Math.abs(2*v*r*rof/eta); // numero di Reynolds
cd=getCd(re);
ax=-0.5*cd*rof*s*vx*v/m;
az=-gamma*g-0.5*cd*rof*s*vz*v/m;
// fine algoritmo di Runge-Kutta IV ordine
t=t+deltaT;
i++;
lxt.add(new Point2D.Float((float)t,(float)x));
lzt.add(new Point2D.Float((float)t,(float)z));
lvxt.add(new Point2D.Float((float)t,(float)vx));
lvzt.add(new Point2D.Float((float)t,(float)vz));
lrt.add(new Point2D.Float((float)t,(float)re));
lct.add(new Point2D.Float((float)t,(float)cd));
lzx.add(new Point2D.Float((float)x,(float)z));
if(z<0)break;
}
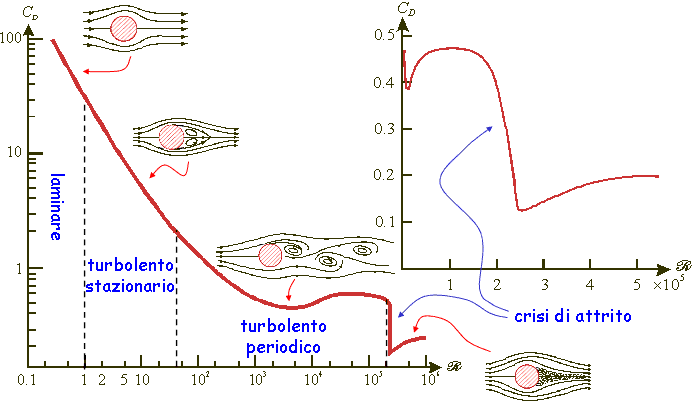
Metodo utilizzato per la
parametrizzazione di CD in funzione del numero di Reynolds:
public double getCd(double re)
{
re=Math.abs(re);
if(re<Double.MIN_VALUE)return 0.; // velocita' 0 => forza 0
if(re<1)return 24.*Math.pow(re,-1);
else if(re<2)return 24.*Math.pow(re,-0.78);
else if(re<5)return 25.6*Math.pow(re,-0.87);
else if(re<10)return 18.25*Math.pow(re,-0.66);
else if(re<20)return 18.62*Math.pow(re,-0.67);
else if(re<50)return 16.57*Math.pow(re,-0.63);
else if(re<100)return 7.01*Math.pow(re,-0.41);
else if(re<200)return 10.6*Math.pow(re,-0.5);
else if(re<500)return 5.62*Math.pow(re,-0.38);
else if(re<2e3)return 2.36*Math.pow(re,-0.24);
else if(re<5e3)return 0.75*Math.pow(re,-0.09);
else if(re<5e4)return 3.04e-16*re*re*re-7.11e-11*re*re+5.56e-6*re+0.322;
else if(re<1.5e5)return -4.4e-12*re*re+9.4e-7*re+0.424;
else if(re<2.5e5)return -1.43e-16*re*re*re+5.12e-11*re*re-6.16e-6*re+0.721;
else if(re<5e5)return 0.005*Math.pow(re,0.274);
else return 0.024*Math.pow(re,0.152);
}
Densità e viscosità di alcuni
fluidi
|
|
densità [kg/m³] |
viscosità [kg m-1 s-1] |
| Aria a 0 °C |
1.25
|
1.82 ·
10-5
|
| Etere a 18 °C |
7.19 ·
102 |
2.38 ·
10-4 |
| Acqua a 0 °C |
1.00 ·
103
|
1.8 ·
10-3 |
| Acqua a 10 °C |
1.00 ·
103 |
1.3 ·
10-3 |
| Acqua a 20 °C |
1.00 ·
103 |
1.0 ·
10-3 |
| Acqua a 30 °C |
1.00 ·
103 |
8 · 10-4 |
| Acqua a 100 °C |
1.00 ·
103 |
2.8 ·
10-5 |
| Alcool a 18 °C |
8.18 ·
102
|
1.25 ·
10-3 |
| Mercurio a 18 °C |
1.3 ·
104
|
1.57 ·
10-2 |
| Olio di ricino a 18 °C |
9.63 ·
102
|
1.11
|
| Glicerina a 2.8 °C |
1.25 ·
103
|
4.22
|
| Glicerina a 18 °C |
1.25 ·
103 |
1.18
|
| Glicerina a 20 °C |
1.25 ·
103 |
0.83
|
| Glicerina a 26.5 °C |
1.25 ·
103 |
0.49
|
Densità di alcuni solidi
|
|
densità [kg/m³] |
Ghiaccio
|
9.17 ·
102
|
Magnesio
|
1.74 ·
103 |
Vetro
|
2.5 ·
103 |
Alluminio
|
2.70 ·
103 |
Zinco
|
7.12 ·
103 |
Stagno
|
7.28 ·
103 |
Ferro
|
7.86 ·
103 |
Ottone
|
8.5 ·
103 |
Bronzo
|
8.8 ·
103 |
Rame
|
8.9 ·
103 |
Argento
|
1.05 ·
104 |
Piombo
|
1.14 ·
104 |
Uranio
|
1.87 ·
104 |
Oro
|
1.94 ·
104 |
Platino
|
2.14 ·
104 |
 Indice Fisica Interattiva
Indice Fisica Interattiva
February 27, 2004, Domenico
Galli
