A-14 Onde e.m. su un cavo coassiale.

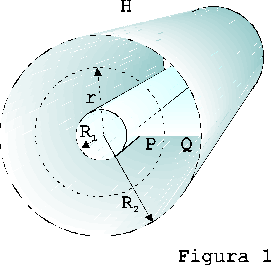
Sia dato un cavo coassiale molto lungo (indefinito); la sezione retta ha forma di cilindri circolari coassiali, di raggi interno ed esterno rispettivamente R₁ e R₂ .

1) - Incominciamo col calcolare la CAPACITÀ’ (per unità di lunghezza) del cavo come quella di un condensatore cilindrico.

Pensiamo una carica uniformemente distribuita sul conduttore interno, con densità l ; su un tratto lungo H la carica vale .

Il modulo del campo elettrico generato da questa carica, a distanza generica r dal centro, si calcola con la legge di Gauss:

quindi

La differenza di potenziale fra le armature vale:

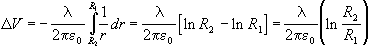
Dalla definizione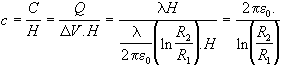

2) - Calcoliamo ora l’INDUTTANZA (ancora per unità di lunghezza) dello stesso cavo.

Il modulo del campo magnetico generato (a distanza r dal centro) dalla corrente I che circola nel cavo, si calcola con la legge di Ampère :

quindi Allora il flusso di B attraverso una sezione longitudinale del cavo, lunga H (per esempio attraverso la superficie piana PQ della figura) vale:

Per definizione di induttanza :

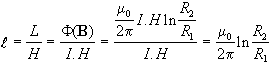
3) Il cavo è un circuito a costanti distribuite: .

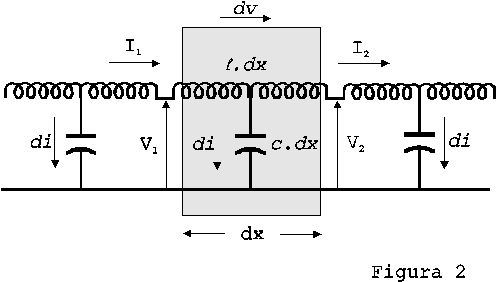
Trascurando la resistenza r (linea senza perdite), lo schema può essere quello di figura 2.

Prendiamo in considerazione una porzione infinitesima di cavo, (una cella) lunga dx (di induttanza e di capacità c.dx)

Sia V₁ la d.d.p. all’ingresso della cella; sia V₂ alla uscita della cella; sia dv la differenza V₂ - V₁: dv è la d.d.p. ai capi della induttanza cioè

Sia I₁ la intensità della corrente entrante; sia I₂ quella uscente; la corrente subisce una variazione (diminuzione) di , costituita dalla carica assorbita (nel tempo dt) dalla capacità c.dx , cioè .

Abbiamo quindi:

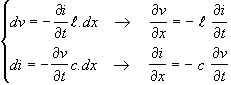
Derivando la prima per x e la seconda per t

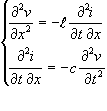
e sostituendo la seconda nella prima (sotto le condizioni del teorema di Schwarz)

otteniamo cioè l’equazione delle onde. Analogamente per la corrente:

Da quanto già calcolato, il quadrato della velocità di propagazione (W²) risulta :

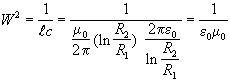cioè = velocità dell’onda e.m. nel vuoto.

Se fra le due lastre fosse interposto un dielettrico isotropo, omogeneo, lineare, di costante dielettrica relativa la velocità diverrebbe

cioè