Sono dati i corpi di capacità termica C₁ e C₂ , alle temperature iniziali T₁ e T₂ (con T₁ < T₂ ), isolati dal resto dell'Universo. Posti direttamente a contatto fra loro si portano (irreversibilmente) alla temperatura intermedia T_x data da (vedi alla fine *** per una traccia del calcolo):

[1]

La variazione di entropia dell'Universo corrispondente a questa trasformazione diviene (essendo T₁₁ e T₂₂ le temperature istantanee):

; da cui integrando

Per mostrare che DS è sempre passiamo dai logaritmi ai numeri .

La condizione 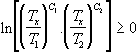diviene quindi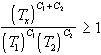

Sostituiamo la T_x fornita dalla [1]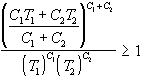

estraendo la radice :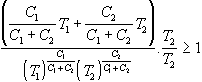

e ancora: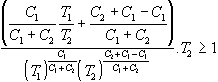

Poniamo ora e

Con passaggi si ottiene: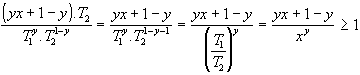

da cui finalmente (x è sempre >0) da discutere : è veramente ?

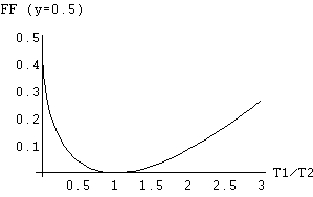
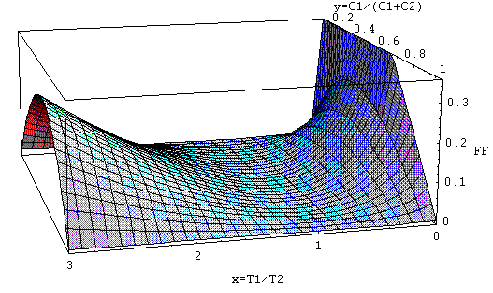
I parametri x ed y sono entrambi sempre > 0 ed entrambi sempre < 1.

Al variare della x risulta quindi che l’espressione FF è sempre >0 e inoltre

Ricordare che la condizione equivale alla condizione .

*** Traccia per calcolare la [1]

Come ipotizzato, il sistema è isolato dal Resto dell'Universo. Per esso possiamo quindi affermare e ; di conseguenza, dal Primo Principio; risulta anche .

Pertanto la somma algebrica delle variazioni dell'energia interna delle due parti in cui è suddiviso il Sistema deve essere uguale a zero; si può quindi scrivere:

da cui, con pochi passaggi, la [1].