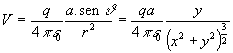
Traccia per le
SOLUZIONI 2000 BOZZANei risultati talvolta si sono qui omessi i passaggi algebrici finali; durante gli esami è però opportuno che i candidati portino a termine (o almeno il più avanti possibile) i calcoli.
Quando il problema comprende dati numerici, la soluzione richiede una risposta numerica.
Si indicheranno con ** eventuali commenti ai procedimenti proposti.
13-7-2000 Elettromagn.
La condizione H>>a ci permette di usare l'approssimazione di dipolo.
Il potenziale del campo E di un dipolo si può scrivere :
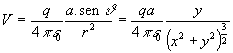
Nel nostro caso, per i punti della guida, la x è costante (e vale ![]() )
)
1) I punti di equilibrio corrispondono ai punti di massimo e minimo del potenziale, per trovare i quali se ne deriva la espressione rispetto a y (la x nel nostro caso è costante) e la si eguaglia a zero; chiamando Z (qui e in seguito) la costante moltiplicativa, si ottiene:
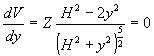 da cui
da cui ![]() e
e ![]() .
.
Sono queste le ordinate dei punti cercati (l'ascissa vale per tutti x=2).
** Si noti che la derivata di V operata qui sopra è la stessa che si esegue per trovare le componenti del campo E = -grad V . La componente x è equilibrata dalla guida; l'annullarsi della derivata di cui sopra corrisponde all'annullarsi della componente y : nei punti trovati il corpo C è sottoposto all'azione di una forza nulla.
2) Per decidere se si tratta di punti di equilibrio stabile o instabile basta ricordare che i primi corrispondono a minimi di energia potenziale, i secondi a punti di massima energia potenziale.
Basta pertanto trovare la derivata seconda di V e ricavarne il segno in corrispondenza dei punti trovati in 1).
A meno del fattore costante (e positivo) Z abbiamo 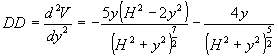
Nei punti in questione troviamo:
in corrispondenza di ![]() è DD < 0 : si tratta di un punto di massimo e quindi di equilibrio instabile;
è DD < 0 : si tratta di un punto di massimo e quindi di equilibrio instabile;
in corrispondenza di ![]() è DD > 0 ; si tratta di un punto di minimo e quindi di equilibrio stabile.
è DD > 0 ; si tratta di un punto di minimo e quindi di equilibrio stabile.
Un grafico della funzione V=f(y) potrebbe essere:……. in cui si vedono bene i punti di massimo e minimo.
ATTENZIONE: Non è stato per ora possibile convertire in HTML il grafico, ottenuto con un programma speciale.
Si consiglia di consultare la versione Word (o quella compressa)
3) Applicando i principi di conservazione dell'energia meccanica in corrispondenza dei punti proposti (P1 e P2) si ricava:
![]() da cui
da cui 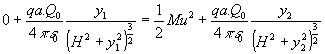 da cui (è y2 = 0) si ricava per la velocità
da cui (è y2 = 0) si ricava per la velocità 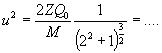 .
.
4) Nel punto P3 (uno dei punti di equilibrio!) la componente Y del campo E è nulla ; resta solo la componente X che viene equilibrata dalla reazione della guida (RG); per cui :
![]() e da questa : RG =
e da questa : RG = 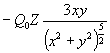
E sostituendo i valori numerici: 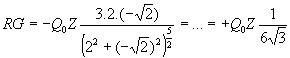
Ottica
1) Quando i due polarizzatori non hanno gli assi paralleli, passa soltanto una componente del campo (legge di Malus) ![]() ovvero
ovvero ![]() per cui
per cui ![]() (non ha importanza che uno dei polarizzatori sia ruotato, rispetto all'altro, verso destra o verso sinistra).
(non ha importanza che uno dei polarizzatori sia ruotato, rispetto all'altro, verso destra o verso sinistra).
2) Quando i due polarizzatori sono disposti ad assi incrociati la intensità della luce emergente è nulla. Per ottenere che la Intensità finale ritorni al massimo, la lamina interposta deve ruotare il piano di polarizzazione della luce emergente dal primo polarizzatore in modo tale da presentarla al secondo polarizzatore polarizzata nella direzione del suo asse: deve cioè ruotare il piano di polarizzazione di ![]() .
.
Una lamina capace di ruotare il piano di polarizzazione di un'onda già polarizzata linearmente (senza alterarne l'ampiezza) è la lamina a mezz'onda. Cerchiamo quindi quale possa essere il minimo spessore di una lamina a mezz'onda.
La differenza dei cammini ottici fra l'onda ordinaria e quella straordinaria (all'interno del cristallo birifrangente di spessore S ) vale : ![]() (dove S è proprio lo spessore cercato)
(dove S è proprio lo spessore cercato)
Affinché la lamina funzioni come lamina a mezz'onda occorre che lo sfasamento fra l'onda ordinaria e quella straordinaria sia ![]() e da questa si ricava
e da questa si ricava ![]()
3) Affinché la lamina a mezz'onda produca una rotazione del piano di polarizzazione pari a ![]() , la direzione dell'asse ottico della lamina deve formare con l'asse di trasmissione del primo polarizzatore un angolo pari a
, la direzione dell'asse ottico della lamina deve formare con l'asse di trasmissione del primo polarizzatore un angolo pari a ![]() . Nel nostro caso si vuole ottenere una rotazione di 90° e l'angolo richiesto vale perciò 45°.
. Nel nostro caso si vuole ottenere una rotazione di 90° e l'angolo richiesto vale perciò 45°.
**Una lamina a quarto d'onda disposta con l'asse ottico a 45° rispetto all'asse di trasmissione del primo polarizzatore, produrrebbe un'onda polarizzata circolarmente. La luce quindi potrebbe anche in questo caso attraversare il secondo polarizzatore ma non con intensità I0 bensì soltanto con intensità ![]() .
.
4) Ovviamente la luce emergente dal sistema, quindi dopo aver attraversato anche il secondo polarizzatore, è polarizzata linearmente secondo la direzione dell'asse di trasmissione del secondo polarizzatore.
Cerchiamo comunque di analizzare ciò che avviene lungo il percorso.
La lamina di spessore S già calcolato (15.10-7 m) se interessata da una radiazione di lunghezza d'onda ![]()
![]() produce uno sfasamento fra onda ordinaria e straordinaria dato da:
produce uno sfasamento fra onda ordinaria e straordinaria dato da:
![]() (
(![]() quindi l'onda ordinaria viaggia più lentamente dell'onda straordinaria e perciò, all'uscita, risulta in ritardo)
quindi l'onda ordinaria viaggia più lentamente dell'onda straordinaria e perciò, all'uscita, risulta in ritardo)
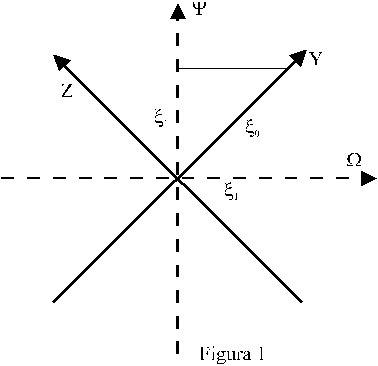
Chiamiamo asse X la direzione di propagazione (uscente dal piano del foglio), asse Y e asse Z le due direzioni (perpendicolari fra loro) secondo le quali sono disposti gli assi di trasmissione dei due polarizzatori (che per ipotesi ora sono incrociati). Dalla risposta 2) abbiamo ancora che l'asse ottico della lamina è disposto lungo la bisettrice dell'angolo fra Y e Z (cioè a 45° rispetto a ciascuno di essi). Chiamiamo asse ![]() l'asse parallelo all'asse ottico della lamina ; e asse
l'asse parallelo all'asse ottico della lamina ; e asse ![]() l'asse ad esso perpendicolare ( Figura 1).
l'asse ad esso perpendicolare ( Figura 1).
Con la disposizione proposta, l'onda che ha attraversato il primo polarizzatore si presenta alla lamina con il piano di polarizzazione parallelo all'asse Y (cioè formante un angolo di 45° con l'asse ottico della lamina stessa - asse![]() ) . Dobbiamo ora scomporre l'ampiezza
) . Dobbiamo ora scomporre l'ampiezza ![]() nelle direzioni parallela e perpendicolare all'asse ottico (cioè lungo
nelle direzioni parallela e perpendicolare all'asse ottico (cioè lungo ![]() e lungo
e lungo ![]() )
)
Se ![]() è l'ampiezza dell'onda che emerge dal primo polarizzatore, con questa disposizione l'ampiezza di ognuna delle componenti (ordinaria e straordinaria) vale (per entrambe)
è l'ampiezza dell'onda che emerge dal primo polarizzatore, con questa disposizione l'ampiezza di ognuna delle componenti (ordinaria e straordinaria) vale (per entrambe) ![]() .
.
All'ingresso della lamina le due componenti sono in fase.
Dopo aver attraversato la lamina, le due componenti (ordinaria e straordinaria) sono sfasate di ![]() e quindi possono essere scritte come :
e quindi possono essere scritte come :
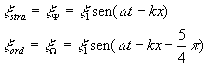 [1]
[1]
Le [1] rappresentano una onda polarizzata ellitticamente .
I due semiassi dell'ellisse sono paralleli rispettivamente agli assi Y e Z della Figura 1 (e formano un angolo di ![]() con l'asse ottico - asse
con l'asse ottico - asse ![]() - della lamina)
- della lamina)
Una rappresentazione dell'ellisse è data in Figura 2 (nella quale gli assi cartesiani (ascisse e ordinate) sono rispettivamente l'asse ![]() e l'asse
e l'asse ![]() e, in unità arbitrarie, si è assunto che sia
e, in unità arbitrarie, si è assunto che sia ![]() e quindi sia
e quindi sia ![]() ).
).
L'ampiezza (![]() ) dell'onda che può attraversare il secondo polarizzatore è rappresentato dalla lunghezza del semiasse parallelo all'asse Z e la intensità
) dell'onda che può attraversare il secondo polarizzatore è rappresentato dalla lunghezza del semiasse parallelo all'asse Z e la intensità ![]() .
.
Quello che precede è quanto si poteva richiedere nella prova d'esame.
COME SOPRA I GRAFICI NON SONO STATI TRADOTTI IN HTML
Nelle pagine seguenti si presenta una discussione più dettagliata per inquadrare meglio la risposta al quesito.
Raffigurazioni di onde polarizzate ellitticamente per vari sfasamenti:
Con sfasamento = 0 Con sfasamento = ![]() Con sfasamento =
Con sfasamento = ![]()
Con sfasamento = ![]() Con sfasamento =
Con sfasamento = ![]() Con sfasamento =
Con sfasamento = ![]()
Con sfasamento = ![]() Con sfasamento =
Con sfasamento = ![]()
Commento alle figure precedenti.

L'onda che incide sulla lamina, è, per ipotesi, polarizzata linearmente lungo la direzione individuata dall'asse Y nella figura 1 (che si ripete qui per comodità); ancora per ipotesi l'asse ottico della lamina è individuato (sempre nella figura 1) dalla direzione dell'asse ![]() (inclinato di 45° rispetto al precedente). Il vettore dell'onda incidente si può scomporre lungo gli assi
(inclinato di 45° rispetto al precedente). Il vettore dell'onda incidente si può scomporre lungo gli assi ![]() e
e ![]() dando luogo rispettivamente all'onda straordinaria e a quella ordinaria (che hanno la stessa ampiezza). Se lo spessore della lamina è tale che, alla sua uscita, fra l'onda ordinaria e quella straordinaria esista:
dando luogo rispettivamente all'onda straordinaria e a quella ordinaria (che hanno la stessa ampiezza). Se lo spessore della lamina è tale che, alla sua uscita, fra l'onda ordinaria e quella straordinaria esista:
Il nostro caso.
Per giungere ad una valutazione numerica del risultato si può infine procedere come segue.
Dobbiamo trovare la lunghezza del semiasse maggiore dell'ellisse.
Si osservi intanto che, con sfasamento (quello dato) = ![]() , la forma dell'ellisse è la stessa di quella che si ottiene con sfasamento =
, la forma dell'ellisse è la stessa di quella che si ottiene con sfasamento = ![]() . Ragioniamo perciò per semplicità in termini di sfasamento =
. Ragioniamo perciò per semplicità in termini di sfasamento = ![]() .
.
I punti estremi dell'asse maggiore si ottengono quando il valore di ![]() soddisfa la relazione:
soddisfa la relazione:
![]() cioè per
cioè per ![]() = 1,17081... radianti (circa 67,5°) ( e per
= 1,17081... radianti (circa 67,5°) ( e per ![]() = - 1,9635...)
= - 1,9635...)
In corrispondenza di questo valore di ![]() , ascissa Y e ordinata Z valgono (entrambe)
, ascissa Y e ordinata Z valgono (entrambe) ![]() (valore comune ad ascissa Y e ordinata Z : ricordare che, nell'ipotesi di sfasamento =
(valore comune ad ascissa Y e ordinata Z : ricordare che, nell'ipotesi di sfasamento = ![]() , il semiasse giace sulla bisettrice del primo quadrante!). La lunghezza H del semiasse risulta pertanto da :
, il semiasse giace sulla bisettrice del primo quadrante!). La lunghezza H del semiasse risulta pertanto da :
![]() intensità dell'onda emergente dal secondo polarizzatore (nelle unità arbitrarie proposte per la figura 2).
intensità dell'onda emergente dal secondo polarizzatore (nelle unità arbitrarie proposte per la figura 2).
**Si noti che se la radiazione incidente avesse lunghezza d'onda ![]() lo sfasamento fra onda ordinaria e straordinaria risulterebbe di
lo sfasamento fra onda ordinaria e straordinaria risulterebbe di ![]() e la polarizzazione risultante all'uscita sarebbe circolare.
e la polarizzazione risultante all'uscita sarebbe circolare.
In quest'ultimo caso, nelle stesse unità, l'intensità varrebbe 0,5.