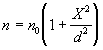 (per la definizione di d vedi qui sotto).
(per la definizione di d vedi qui sotto).Problemi proposti agli Esami nell’anno1998
Fisica Generale II (A. Gandolfi)
23-1-1998
Elettrom. SoluzioneUna lastra L di materiale conduttore di resistività
r, è sagomata a forma di corona circolare di raggi R1 e R2 (>R1) e spessore H (molto sottile)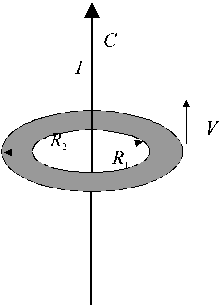
Perpendicolare al piano della lastra e passante per il centro della corona circolare è posto un conduttore filiforme C, rettilineo, molto lungo, percorso da una corrente di intensità costante I.
La lastra L trasla con velocità costante V lungo il conduttore C , mantenendosi perpendicolare ad esso e rimanendo centrata su esso.
Calcolare:
Si trascurino eventuali fenomeni di autoinduzione
23-1-1998
Ottica - SoluzioneSi realizza un esperimento di interferenza (alla Young) usando uno schermo piano opaco nel quale sono praticate le due fenditure (molto sottili) S1 , S2 , distanti fra loro H (=1 mm). Lo schermo viene illuminato da retro con luce monocromatica di lunghezza d’onda
l (= 5.10-7 m ) . Il fronte d’onda piano della luce incidente forma con lo schermo opaco un angoloLa figura di interferenza viene raccolta su un secondo schermo bianco, piano, parallelo allo schermo che porta le fenditure e distante D (=5 m) da esso.
Si ricopre la fenditura S1 con una sottile lastra di plastica trasparente a facce piane parallele, facce a loro volta parallele allo schermo opaco; l’indice di rifrazione del materiale di cui è formata la lastra varia con il generico spessore X (perpendicolarmente alle superfici piane) secondo la legge 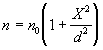 (per la definizione di d vedi qui sotto).
(per la definizione di d vedi qui sotto).
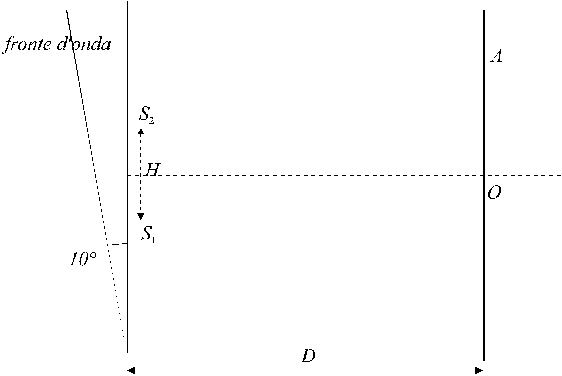
20 - 2 - 1998
Elettromagnetismo . Soluzione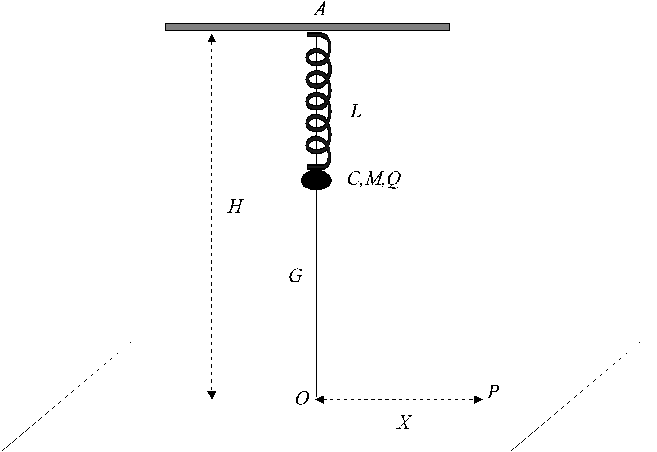
E’ dato un corpo C molto piccolo, di massa M , che porta una carica +Q Esso può scorrere senza attrito lungo una guida verticale G ( nella quale lo si può pensare infilato come un anellino).
Il corpo C è fissato all’estremo libero di una molla (coassiale con la guida G e di costante elastica opportuna), il cui secondo estremo è ancorato ad un vincolo A fisso e rigido. La lunghezza a riposo della molla è L.
Alla distanza H sotto A è sistemato un piano orizzontale perfettamente conduttore collegato al potenziale di terra (V=0). Nelle condizioni di equilibrio la distanza di C dal piano vale X.
In queste condizioni determinare:
Se successivamente si abbandona (da fermo) il corpo C dopo averlo portato a distanza Y dal piano, determinare:
Eseguire i calcoli con L=1; H = 5; M=0,1; g=10; X=2; Y= 3 ; Z= 2 e ![]() espressi tutti in unità del S.I.
espressi tutti in unità del S.I.
20 - 2 - 1998
Ottica SoluzioneUn reticolo di diffrazione, realizzato su una lastrina quadrata di lato 2 cm , è costruito in modo da risolvere al limite il doppietto del sodio (*) allo spettro del primo ordine.
Esso viene usato per analizzare (su uno schermo posto a distanza D = 2 m e parallelo al piano del reticolo) la luce di due sorgenti A e B di onde piane che si propagano perpendicolarmente al piano del reticolo e le cui lunghezze d’onda sono rispettivamente
lA = 5092 Å e lB = 5601 Å.Determinare:
(*) Si ricorda che il doppietto del sodio è costituito da due righe di lunghezze d’onda
l
1 = 5890 Å e l2 =5896 Å14 - 3 - 1998
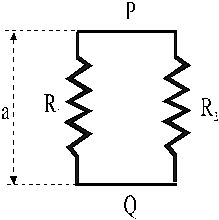
Elettrom. . SoluzioneDato il circuito di figura determinare (in condizioni di regime) :
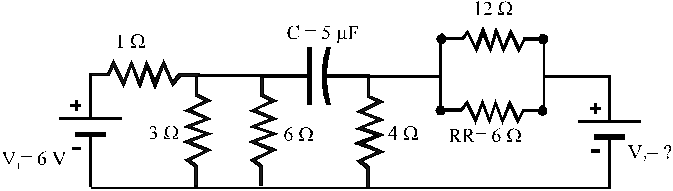
14 - 3 - 1998
Ottica A Soluzione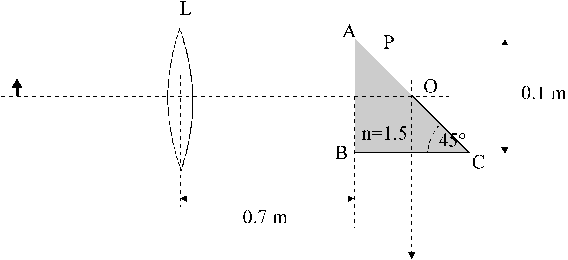
E’ dato il sistema di figura in cui L è una lente sottile, convergente (raggi di curvatura R=1 m; indice di rifrazione n = 1.5 ) ; P è un prisma costruito con lo stesso vetro della lente. Angoli e distanze sono quelli indicati in figura.
Dato un oggetto all’infinito (alla sinistra della lente)
Ottica B . Soluzione
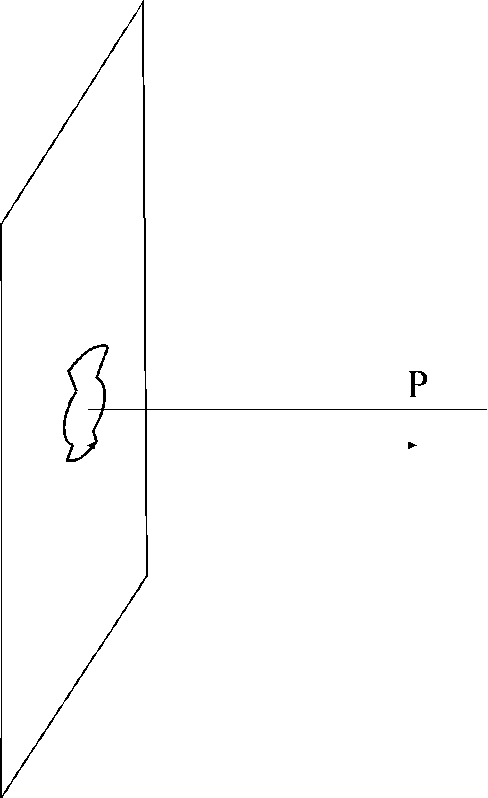
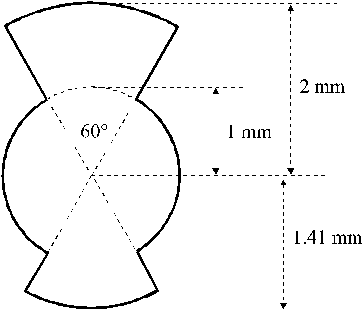
Uno schermo opaco piano porta un’apertura sagomata come in figura: un foro circolare con due "appendici" da bande opposte (le dimensioni sono date in figura). Lo schermo viene illuminato dal retro da un’onda piana, monocromatica (![]() Å) con fronte d’onda parallelo allo schermo stesso.
Å) con fronte d’onda parallelo allo schermo stesso.
Chiamando ![]() l’ampiezza della perturbazione in P in assenza di schermo, determinare :
l’ampiezza della perturbazione in P in assenza di schermo, determinare :
3) l’ampiezza nel punto P (sull’asse del foro circolare e distante dal centro del foro 2 m) dell’onda diffratta dall’apertura ;
18 - 4 - 1998
Elettromagnetismo SoluzioneSi faccia riferimento al sistema di figura.
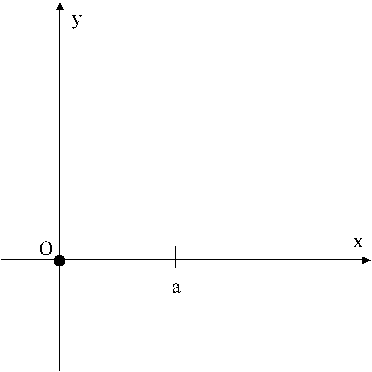
E’ data una carica puntiforme Q che viene fissata nell’origine O.
Un oggetto puntiforme (di massa M e carica Q1) viene lanciato dal punto P di coordinate (![]() ) con velocità V (
) con velocità V (![]() ).
).
Chiamando G il punto della traiettoria descritta da P che si trova a minima distanza da O e chiamando R questa minima distanza, determinare:
Eseguire i calcoli con i seguenti valori (espressi in unità S.I.)
M = 1 ; ![]() ; V0 = 2 ; a = 5 , Q1 = Q .
; V0 = 2 ; a = 5 , Q1 = Q .
Ottica 18-4-1998 Soluzione
Una onda piana, monocromatica, polarizzata linearmente in direzione perpendicolare al piano del disegno, viene in qualche modo sdoppiata e le due onde risultanti (A e B, entrambe di ampiezza ![]() ) procedono parallele, mantenendosi per ipotesi coerenti tra loro.
) procedono parallele, mantenendosi per ipotesi coerenti tra loro.
Sul cammino dell’onda A è posta una lamina a quarto d’onda LA il cui asse ottico è perpendicolare al piano del disegno e, di seguito, una lastrina trasparente SA (per la quale vedi dopo); sul cammino dell’onda B è posta una lamina a quarto d’onda LB il cui asse ottico è parallelo al piano del disegno e, di seguito, una lastrina trasparente SB . Le onde vengono quindi sovrapposte nel punto P .
Discutere come si presenta l’onda (ampiezza e polarizzazione) nel punto P nei seguenti casi:
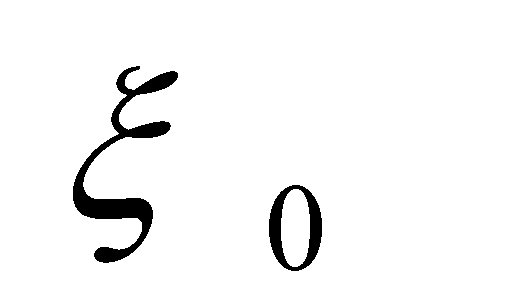
16 -5 - 1998
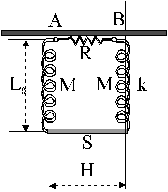
Elettromagnetismo SoluzioneNella figura sono dati:
Il circuito è disposto in un piano verticale perpendicolare al campo B e la sbarretta S è inizialmente in quiete con le molle in posizione di riposo. Partendo da questa condizione si abbandona la sbarretta S , lasciandola libera di muoversi (il circuito, durante il moto, resta in un piano verticale). Determinare:
1) la potenza istantanea dissipata nella resistenza R (in un istante generico, chiamando provvisoriamente V la velocità posseduta in quell’istante da S - si potrà eventualmente esplicitare il valore di V dopo aver risposto alla domanda 3 ); [4]
2) l’energia dissipata nella resistenza R dopo un tempo opportunamente lungo (al limite infinito); [5]
3) la legge oraria del moto della sbarretta , spiegando di che tipo di moto si tratta. [6]
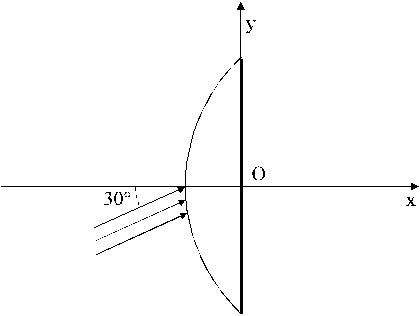
Si trascurino i fenomeni di autoinduzione e di irraggiamento.
16 - 5 - 1998
Ottica A SoluzioneE’ data una lente sottile costituita da una faccia convessa ed una faccia piana.
Il raggio di curvatura della superficie sferica è R e l’indice di rifrazione del vetro è n.
La faccia piana è argentata.
Un fascio di raggi paralleli incide sulla lente come in figura.
Eseguire i calcoli con R =0.5 m e n = 1.5
Ottica B Soluzione
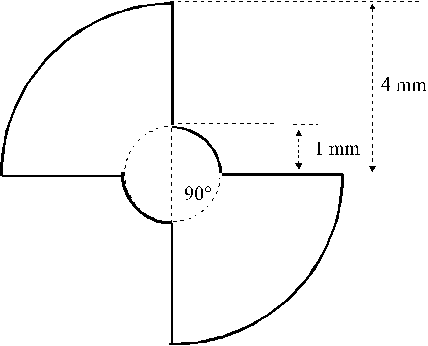
Uno schermo opaco piano porta un’apertura sagomata come in figura: un foro circolare con due "appendici" da bande opposte (le dimensioni sono date in figura). Lo schermo viene illuminato dal retro da un’onda piana, monocromatica (![]() Å) con fronte d’onda parallelo allo schermo stesso.
Å) con fronte d’onda parallelo allo schermo stesso.
Chiamando ![]() l’ampiezza della perturbazione in P (e Q) in assenza di schermo, determinare l’ampiezza dell’onda diffratta dall’apertura :
l’ampiezza della perturbazione in P (e Q) in assenza di schermo, determinare l’ampiezza dell’onda diffratta dall’apertura :
2) nel punto P sull’asse del foro circolare e distante dallo schermo 1,25 m) [4 p]
3) nel punto Q (sull’asse del foro circolare e distante dallo schermo 10 m) [6 p]
16 -6 - 1998
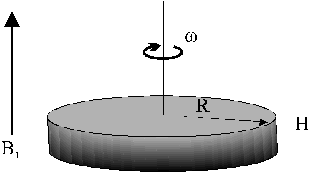
Elettromagnetismo SoluzioneUn disco che ha forma di cilindro circolare retto (di raggio R e spessore [sottile] H) è costituito di materiale dielettrico isotropo, omogeneo, lineare (costante dielettrica relativa
er); esso è immerso in un campo di induzione magnetica B1 costante, uniforme e parallelo all’asse del disco. Il disco ruota in senso orario attorno al proprio asse (asse del cilindro) con velocità angolare w costante.Determinare:
1)- la densità di volume ![]() della carica di polarizzazione presente all’interno del disco ; [5 punti]
della carica di polarizzazione presente all’interno del disco ; [5 punti]
2)- la carica QP di polarizzazione presente sulla superficie laterale del disco; [5 p]
3)- modulo, direzione e verso del campo di induzione magnetica B4 generato sull’asse del disco dalla rotazione del disco stesso . [5 p]
Si trascurino i fenomeni di autoinduzione e di irraggiamento.
16 - 6 - 1998
Ottica . SoluzioneUn’onda piana monocromatica (lunghezza d’onda
l) incide perpendicolarmente su uno schermo piano opaco sul quale sono praticate 5 lunghe fenditure rettilinee identiche e parallele tra loro. La larghezza delle fenditure è b e la distanza fra i centri delle fenditure è a (con a = 2b ). SiaDeterminare:
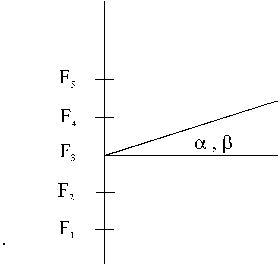
Supponiamo ora di chiudere la fenditura centrale (F3 di figura) ; determinare:
4) Supponendo di chiudere anche la quarta fenditura (F4), valutare l’ampiezza della perturbazione sullo schermo (sempre posto all’infinito) sotto l’angolo ![]() . [4 p]
. [4 p]
9 - 7 - 1998
Elettromagnetismo SoluzioneUn corpo puntiforme con carica Q0 è vincolato nell’origine O di un sistema cartesiano. Attorno ad esso, con traiettoria stabile, si muove, di moto periodico, un altro corpo puntiforme di massa M e carica q . La minima distanza di q dall’origine è R1 e V1 è la sua velocità in questa configurazione.
Si trascurino le interazioni gravitazionali e l’irraggiamento.
Calcolare inoltre:
2) l’energia del sistema [2 p.]
3) la massima distanza R2 da O a cui si può portare q durante il suo moto. [5 p.]
4) il lavoro che un agente esterno deve compiere per portare q su un’orbita circolare stabile di raggio R3 =2.R2 [6 p.]
9 - 7 - 1998
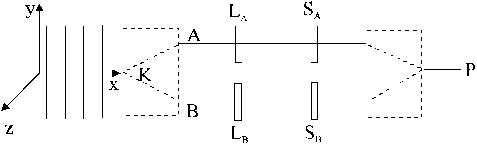
Ottica SoluzioneNel sistema cartesiano destrorso di figura, un’onda piana, monocromatica, polarizzata circolarmente (per es. in senso orario) si propaga nel verso positivo dell’asse X; essa viene in qualche modo sdoppiata in K e le due onde risultanti (A e B, entrambe di ampiezza ![]() ) procedono parallele, restando per ipotesi coerenti fra loro.
) procedono parallele, restando per ipotesi coerenti fra loro.
Sul cammino dell’onda A sono poste una lastrina trasparente LA e, di seguito, una lastrina pure trasparente SA (per le quali vedi dopo); sul cammino dell’onda B sono poste, di seguito, una lastrina trasparente LB ed una SB (anche per queste vedi dopo). Le onde vengono quindi sovrapposte nel punto P . Le lamine a quarto d’onda e a mezz’onda sono costituite di calcite.
Discutere come si presenta l’onda risultante (ampiezza e polarizzazione) nel punto P nei seguenti casi:
10 - 9 - 1998
Elettromagnetismo A Soluzione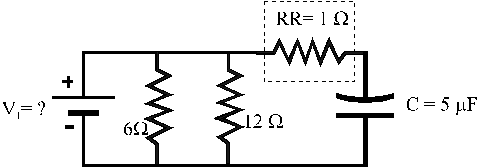
Nel circuito di figura
Elettromagnetismo B Soluzione
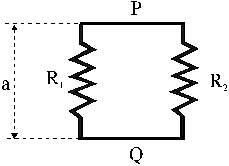
. Una spira quadrata di lato a è immersa in un campo di induzione magnetica uniforme![]() dove n è il versore normale al piano della spira. Il lato destro e quello sinistro della spira hanno resistenze differenti R1 ed R2 (la resistenza degli altri lati è trascurabile).
dove n è il versore normale al piano della spira. Il lato destro e quello sinistro della spira hanno resistenze differenti R1 ed R2 (la resistenza degli altri lati è trascurabile).
Trascurare i fenomeni di autoinduzione e di irraggiamento
10 - 9 - 1998
Ottica SoluzioneSono date 8 sorgenti puntiformi di onde monocromatiche, di uguale ampiezza ![]() e lunghezza d’onda l; le sorgenti sono isotrope, coerenti, in fase fra loro, disposte equispaziate su una retta; la distanza fra le sorgenti è a . Si osserva a grande distanza l’interferenza fra le onde emesse, prendendo come riferimento la direzione perpendicolare al segmento che unisce le sorgenti.
e lunghezza d’onda l; le sorgenti sono isotrope, coerenti, in fase fra loro, disposte equispaziate su una retta; la distanza fra le sorgenti è a . Si osserva a grande distanza l’interferenza fra le onde emesse, prendendo come riferimento la direzione perpendicolare al segmento che unisce le sorgenti.
Calcolare:
Supponiamo ora che siano attive solo le sorgenti F1 , F2 , F3 , F5 , F6 , F7 (oscurando F4 e F8 ); determinare:
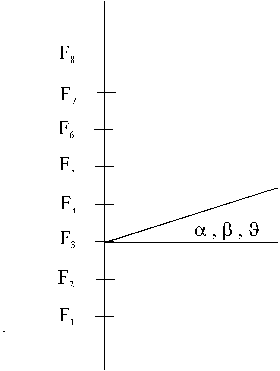
Si supponga di avere solo le sorgenti F1 , F2 , F3 , F6 , F7 , F8 (oscurando F4 e F5 );
26 - 9 - 1998
Elettromagnetismo A Soluzione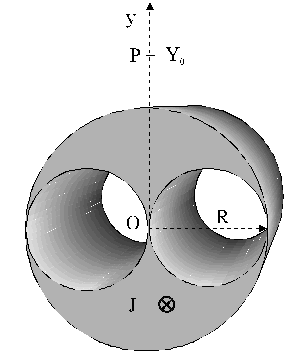
In un conduttore rettilineo indefinito di forma cilindrica, a sezione retta circolare di raggio R, sono praticate, per tutta la sua lunghezza, due cavità cilindriche, identiche, di sezione retta pure circolare, di raggio ![]() (vedi figura). La parte piena del conduttore (grigia in figura) è percorsa da una corrente elettrica costante, uniforme, di densità J , parallela all’asse del cilindro, entrante nel foglio.
(vedi figura). La parte piena del conduttore (grigia in figura) è percorsa da una corrente elettrica costante, uniforme, di densità J , parallela all’asse del cilindro, entrante nel foglio.
Elettromagnetismo B . Soluzione
E’ dato un condensatore in aria, a facce piane parallele, quadrate di lato L e distanti 3H. Esso è stato caricato con un generatore di f.e.m. V0 e quindi scollegato dal generatore.
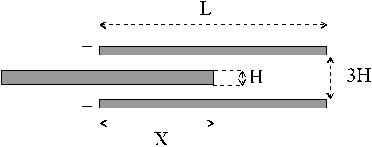
Tra le armature del condensatore viene parzialmente inserita (per un tratto ![]() ) una lastra conduttrice [pure quadrata di lato L] inizialmente scarica, lasciando spessori d’aria H dalle due parti (vedi figura).
) una lastra conduttrice [pure quadrata di lato L] inizialmente scarica, lasciando spessori d’aria H dalle due parti (vedi figura).
Con le consuete approssimazioni applicate ai condensatori a facce piane, calcolare:
26 - 9 - 1998
Ottica SoluzioneUn reticolo di diffrazione è costituito da una lastrina quadrata di 1 cm di lato su cui sono praticate 1000 fenditure larghe b . Per osservare la figura di diffrazione in campo lontano (diffrazione di Fraunhofer) si pone a valle del reticolo una lente sottile piano-convessa (indice di rifrazione n=1,5 , raggio di curvatura R ). La figura di diffrazione viene osservata su uno schermo posto nel piano focale della lente perpendicolarmente all’asse ottico della stessa.
Il reticolo è illuminato normalmente da un fascio di luce non monocromatico; sullo schermo, oltre al massimo centrale (massimo di ordine zero), si osservano le righe dello spettro. Tra le righe appartenenti al massimo del primo ordine se ne osserva una prima (A), situata a distanza 8 cm dal massimo centrale e una seconda (B), situata a distanza 12 cm (sempre dal massimo centrale)
Calcolare:
Torna in Testa a queste Pagine