APPUNTI DALLE LEZIONI DELL'A.A. 2001-2002
Statistica Sanitaria
Dott.ssa
. Elena Baldi9/11/01
A Florence Nightingale si riconosce il merito di avere impostato per prima il discorso dell’Evidence Based Nursing, che è nata come disciplina da pochi anni e che sarà il nursing del futuro.
È indispensabile un approccio quantitativo se vogliamo che la professione sia una vera scienza.
Le statistiche da fare quando si entra in un reparto sono:
Questi dati non vengono definiti misure, visto che per misura s’intende un rapporto tra un fenomeno e la sua unità di misura.
I dati qualitativi sono quelli che si esprimono con modalità, cioè modo di presentarsi.
Ci sono informazioni:
Ogni unità statistica puo' possedere una o più di queste informazioni
Ad es. il sig. Rossi puo' pesare 85 Kg (misura), puo' esser maschio (modalità), puo' avere un diabete mellito grave (rango)
.I fenomeni si studiano sempre in due tempi.
I dati sono sintetici, le unità sono informazioni di tipo analitico.
Frequenza relativa e frequenza percentuale
La frequenza percentuale è più sintetica e immediata.
Frequenza assoluta = numero di unità che hanno quel rango o modalità
Frequenza relativa = numero di unità che hanno quel rango o modalità diviso per l’effettivo numero di pazienti, ad esempio: 18 maschi in una classe di 32 allievi, freq. Relativa maschi = 18/32=0,5625 La statistica, in genere, si fa con i denominatori.
Frequenza percentuale = frequenza relativa rapportata a cento.
Il termine "statistica" deriva da stato, perché puo' essere uno strumento di governo e la prima risale all’impero romano (la Madonna si stava recando a Gerusalemme per iscriversi al censimento quando partorì).
Scopo della statistica è dare un'informazione sintetica, completa e corretta.
Le informazioni si possono graficare tramite un istogramma, dove sull’asse delle ascisse è convenzione internazionale avere il fenomeno che sto studiando.
Altro modo di graficare è lo schema a torta, completo di una legenda. Questa rappresentazione è quella più immediata visivamente, per i dati qualitativi o semiquantitativi
Il limite delle rappresentazioni grafiche è che non ci
si possono fare ulteriori elaborazioni.
16/11/01
Sintesi numerica
Ci sono diversi modi per fare una sintesi numerica:
Indicatori di tendenza centrale
Con lo stesso sistema, dividendo
le misure in quattro parti equivalenti, otteniamo dei valori detti quartili. Il primo quartile è l’indicatore che divide il primo quarto di misure più piccole dalle altre, mentre la mediana corrisponde al secondo quartile. Il terzo quartile da un lato divide i 3/4 di misure più picole dalle altre, dall'altro lato delimita il 1/4 di misure più grandiL’intervallo interquartile corrisponde alla differenza tra terzo quartile e il primo.
Per una sintesi:
Un altro indicatore di dispersione è il range o campo di variazione che si ottiene facendo la differenza tra il valore massimo e quello minimo di una insieme di misure.
In sintesi
19/11/2001
Quando cerchiamo di riassumere i fenomeni dobbiamo sempre dare un indicatore di tendenza centrale, ma da soli questi non rappresentano in modo completo la realtà (statistica = sintesi completa e corretta) quindi bisogna aggiungere gli indicatori di variabilità.
Per calcolare la variabilità se come indicatore di tendenza centrale usiamo la media, bisogna vedere quanto sono distanti le misure dal valore medio, cioè gli scarti dalla media.
|
Numeri |
1 |
2 |
3 |
4 |
5 |
|
Scarti |
-2 |
-1 |
0 |
+1 |
+2 |
Faccio la
Media degli scarti = (-2-1+0+1+2) /5 = 0Proprietà fondamentale della media aritmetica: la somma degli scarti degli elementi di un insieme deve essere zero.
Allora, come si fa? Il modo migliore di procedere per eliminare i segni algebrici è elevare al quadrato gli scarti.
Varianza = media della somma degli scarti al quadrato
Deviazione standard = radice quadrata della varianza
Dati quantitativi
Le cornici indicano "matrimoni" indissolubili tra indicatori di tendenza centrale e di dispersione
L’indicatore di variabilità dei dati qualitativi è l’indice di eterogeneità di Gini.
Serve soprattutto quando si hanno tantissime modalità ognuna con la propria frequenza: elencarle tutte non aiuterebbe la sintesi.
In questi casi si puo' indicare la frequenza modale (la frequenza maggiore) e l'indice di eterogeneità di Gini.
30/11/01
K. F. Gauss (1777 — 1855) fu un fisico che si occupò di studiare gli errori che si compiono nel misurare.
La curva a campana di Gauss è la curva dell’errore insito in ogni misura.
La curva è simmetrica attorno alla media e non tocca mai gli assi cartesiani se non all'infinito (tende asintoticamente agli assi cartesiani).
Le informazioni possono esser riassunte anche con grafici, ma
il difetto del grafico è che non si presta ad ulteriori elaborazioni dei dati.
Quando si vogliano fare delle programmazioni
è importante sapere quanti dati sono compresi entro certi limiti e con l'equazione di Gauss lo si puo' fare con grande precisione.Equazione di Gauss
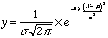
sembra complicatissima, ma in fin dei conti esprime qualcosa di analogo a quello che tutti abbiamo studiato a scuola: y=a+bx, che si poteva disegnare sugli assi cartesiani come una retta. Per ogni valore di x permetteva di conoscere y.
Questa equazione si puo' disegnare come una curva a campana.
In fondo è piena di numeri fissi:
1/Ã2p = 0,399, circa = 0,4
e = 1,2
e poi, sapendo che
s =
deviazione standardm =
media(x - m) = scarto dalla media,
questa equazione dipende dalla deviazione standard, dalla variabilità e dallo scarto dalla media.
Chi l'ha fatto a scuola lo sa, chi non lo sa ci deve credere che con il calcolo integrale è possibile conoscere l'area sottostante a due punti x1 e x2 della curva.
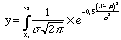
Se x1 = media -1,96 deviazioni standard e x2 = media +1,96 deviazioni standard, y viene sempre =0,95
Se x1 = media -2,57 deviazioni standard e x2 = media +2,57 deviazioni standard, y viene sempre =0,99
Questo significa che entro la
Media +/- 1,96 d.s. sono compresi il 95% delle misure
Media +/- 2,57 d.s. sono compresi il 99% delle misure
Questi concetti, vengono dimostrati dallo studio della curva normale standardizzata.
Standardizzare = misurare un fenomeno in deviazioni (o, vedremo poi, errori) standard
LA DEVIAZIONE O L'ERRORE STANDARD, CIOÈ GLI INDICATORI DI VARIABILITÀ, VENGONO ASSUNTI DALLA STATISTICA COME UNITÀ DI MISURA!!!
Tragico, ma vero.
Decenni fa, per ovviare alla difficoltà di fare sempre quel calcolo integrale, pensarono di considerare:
m
=0 e s=1e di trasformare ogni misura x in "scarto di quella misura dalla media, x s
L'equazione di Gauss diventa molto più abbordabile:
![]()
Con i logaritmi diventa facile risolverla,
tanto è vero che un tempo tutti i possibili valori venivano riassunti in una paginetta di calcoli già fatti e che ora quegli stessi valori si trovano memorizzati nei computer. Sono alla base di cose molto interessanti, come gli-Intervalli di confidenza
-Il controllo di qualità
-Bench marking = provvedere al miglioramento della propria qualità rispetto agli altri.
4/12/2001
Dr. William Sealey Gosset (13/6/1876 — 16/10/1937)
Chimico presso le birrerie Guinness, statistico di importanza storica sotto lo pseudonimo di "student", da cui test di Student.
Con il campionamento non sempre si fa centro anche se è indispensabilein medicina: gli esseri umani sono 6 miliardi.
La statistica medica e sanitaria tendono a sintetizzare i fenomeni correttamente e completamente. Ottengono questo attraverso la raccolta e l’analisi,delle unità statistiche.
Le unità statistiche si possono raccogliere
tramite misura o valutazione delle modalità di presentazione delle unità stesse. Già in questa fase vi posson essere errori perché si può sbagliare nella misura ed anche nella valutazione delle modalità.
Le unità vengono poi riassunte in
dati statistici, che sono per:Anche in questa fase si possono commettere errori, se non si scelgono gli indicatori giusti.
Anche con tutto l’universo di dati gli errori sono inevitabili.
Con il campionamento le faccende si complicano perché il campionamento porta a una visione distorta della realtà.
Per ridurre al minimo gli errori il campione dovrebbe essere:
In medicina o in nursing è quasi impossibile. Si cerca di ovviare ai problemi:
di non omogeneità con la
Stratificazione = prima bisognaindividuare le variabili principali che influenzano la ricerca: ad esempio bisogna quasi sempre stratificare secondo il sesso o secondo le fasce di età..All’interno di ogni strato si estraggono a caso (=random) una % di persone secondo quanto si è deciso in precedenza.
La randomizzazione sarebbe fatta con l'intento di garantire ad ogni elemento dell'universo la stessa probabilità di far parte del campione. Questo in campo sanitario è francamente impossibile: non si puo' estrarre due volte una persona per sottoporla a appendicectomia!!!
La randomizzazione, che è un processo molto complicato e costoso, può essere:
Il campionamento sistematico è molto soggetto ad errori. Si puo' fare solo per ricerche poco importanti. Un esempio puo' essere: scelgo solo le persone nate di venerdì (già ho selezionato più o meno 1/7 della popolazione)
Anche il campionamento più corretto, comunque, è un bel problema. Immaginiamo di vedere cosa succederebbe campionando 5 a 5 questo universo noto:
Universo
|
Misure |
Frequenza |
|
1 kg |
1 |
|
2 kg |
2 |
|
3 kg |
3 |
|
4 kg |
4 |
|
5 kg |
5 |
|
6 kg |
4 |
|
7 kg |
3 |
|
8 kg |
2 |
|
9 kg |
1 |
|
tot |
25 |
Media = 5 kg; D.S. = 2,04 kg; N = 25
Mediana = 5 kg; S.I. = 6,5 kg; N = 25
Moda = 5 kg; range = 8 kg, N = 25
Campionamento al 20%
1° caso
|
Misure |
Frequenza |
|
1 kg |
|
|
2 kg |
|
|
3 kg |
|
|
4 kg |
1 |
|
5 kg |
|
|
6 kg |
1 |
|
7 kg |
2 |
|
8 kg |
1 |
|
9 kg |
Tot = 5; Media = 6,4; D.S. = 1,571 e se mi capita questo campione, io penso che la media sia 6,4, invece che 5
2° caso
|
Misure |
Frequenza |
|
1 kg |
|
|
2 kg |
|
|
3 kg |
|
|
4 kg |
|
|
5 kg |
2 |
|
6 kg |
|
|
7 kg |
1 |
|
8 kg |
1 |
|
9 kg |
1 |
Tot = 5; media = 6,2; D.S. = 1,789 e se mi capita questo campione, io penso che la media sia 6,2, invece che 5
Ecc. ecc.ripetendo per gli oltre 15 000 possibili campioni, si ottengono
risultati tutti diversi.
Il Gosset fece proprio questa prova e poi riportò le varie medie che otteneva sugli assi cartesiani. Ottenne una curva che assomigliava a una gaussiana, ma era un po' più stretta di quella dell'universo di partenza.
Il campo di variazione delle misure dell'universa va da 1 a 9
Campo di variazione delle possibili medie campionarie va da 2,2 — 7,8 => tende a una gaussiana più stretta
L'indicatore di dispersione di questa curva è simile alla deviazione standard, ma un po' più piccolo, perché va diviso per la radice quadrata della numerosità campionaria (nel nosro esempio, radice di 5)
Questo indicatore viene chiamato
è l’errore standard della media => D.S. / Ãn (numerosità del campione)D.S. = ÷(x - m)2/N
e. s. = D.S./Ãn(numerosità del campione)
7/12/2001
Nelle elezioni , quando fanno le previsioni su chi vince man mano che si fa lo spoglio dei voti, spesso si sente dire che la forbice si stringe. La forbice si stringe man mano che i voti spogliati si avvicinano al totale, cioè all'universo dei votanti.
Quando comunicano i risultati delle prime sezioni è come se dessero i risultati di un campione di tutti gli italiani. Questo parlare di "forbic" indica che si riconosce che questa è solo una STIMA.
Stima = processo per cercare di conoscere la realtà (le tendenze centrali di un fenomeno) in anticipo. In alcuni casi, come sempre in nursing e in medicina tutta la nostra conoscenza avviene sempre e solo tramite la conoscenza di campioni di individui, cioè per STIMA
Esempio:
Descrittiva delle azotemie di 600 pazienti
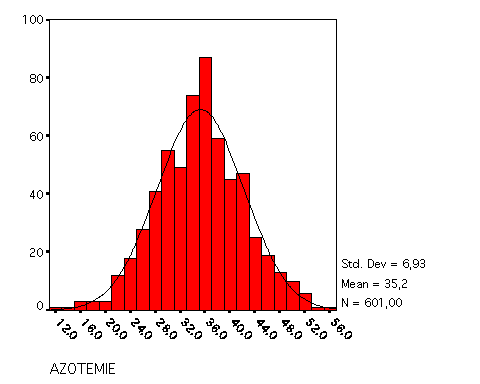
La mente per capire ha bisogno di riassumere queste 601 informazioni
In statistica medica, l’apice della curva di Gauss è molto importante, perche indica la tendenza centrale dei fenomeni ed è quella che interessa chi debba organizzare un servizio, chi voglia cominciare a conoscere un fenomeno medico ancora da scoprire. La curva rappresenta la seguente formula:
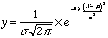
Fa un po' spavento a vederla, ma la si osserva bene, senza false paure, è piena di numeri fissi.
Vi sono soltanto due variabili:
Togliendosi tutte le paure e applicando il calcolo integrale è stato possibili conoscere i valori dell'area che sta al di sotto della curva di Gauss..
Sotto a tutta la curva, per definizione, è compresa un'area unitaria (=1)
Inoltre sempre, costantemente, ogni volta che si parli di curve gaussiane o simili a gauss, standardizzando la curva, si impara che:
La normale standardizzata
si ottiene misurando in deviazioni standard gli scarti dalla media delle singole misure.
x z = x -m/s
(è come dire che entro la media +1deviazione standard ed entro la media -1deviazione standard si trova compresa il 68,3% di tutta l'area, cioè 0,683)
|
Deviazione standard |
% di unità statistiche |
|
|
Media |
+1 |
68,3% |
|
Media |
-1 |
|
|
Media |
+2 |
95,5% |
|
Media |
-2 |
|
|
Media |
+3 |
99,7% |
|
Media |
-3 |
Su questa tabella si basano i controlli di qualità
Questa tabella è utile per i controlli di qualità (prevedere l'acquisto di materiali, per esempio; valutare se negli ultimi tempi si sono avute più infezioni ospedialiere che di norma).
Di norma, vuole dire normale (di Gauss), c'avete mai pensato?
Un altro uso importante della normale standardizzata è per valutare i limiti di confidenza.
Tabella dei limiti di confidenza
|
Indicatori di dispersione (errori o deviazioni standard) |
Valore dell’integrale |
% di unità statistiche comprese |
|
Media + 1,96 |
0,95 |
95% |
|
Media — 1,96 |
||
|
Media + 2,57 |
0,98984 |
99 % |
|
Media — 2,57 |
||
|
Media + 0,67 |
0,5 |
50 % |
|
Media — 0,67 |
I limiti di confidenza permettono di conoscere la stima sono più esatti (95%, 99% tondi, perché utilizzabili in campo scientifico, più che in campo pratico, come accade per i controlli di qualità.
La statistica usa numeri e strumenti matematici, adattandoli al proprio universo, reale e materiale.
L'adattamento è difficile!
I fenomeni sono conoscibili in medicina solo per stima e la conoscenza è sempre parziale.
Siamo sei miliardi, non si possono conoscere tutti i fenomeni completamente, la conoscenza è sempre approssimativa.
Come fare la stima è un argomento studiato a fondo da Gosset (quello del t di Student) .
Questi prese un universo noto di 25 misure,
poi si calcolò le medie di tutti gli oltre 15000 campioni di 5 misurepossibili (scelti regolarmente random).Rappresentando questi valori medi in un grafico trovò che si distribuivano secondo una curva di Gauss ma leggermente più stretta e alta di quella classica (curva di distribuzione delle medie campionarie).
Che peccato sarebbe stato non poter usare quella tabellina sopra indicata, soltanto perché la curva di distribuzione delle medie campionarie non era proprio identica a quella di Gauss!!!
Ma quando si conosce bene la matematica….
Per fare la stima di una tendenza centrale universale tramite campionamento occorre conoscere l'errore standard, che è l'indicatore di dispersione delle medie campionarie possibili. Questo errore è tanto più grande quanto più
E' possibile utilizzare la tabellina di cui sopra, modificando un po' quell'indicatore di dispersione che ci serve come unità di misure.
|
Indicatore dispersione curva di Gauss |
Indicatore dispersione distribuzione medie campionarie |
|
|
|
N.B.:
s è circa uguale a d.s.. s si riferisce all'universo, d.s. al campione. Ovviamenteds>es, così come la curva di Gauss è più dispersa di quella delle medie campionarie.
Si è rimpicciolita l'unità di misura, della normale standardizzata, così si puo' usare la tabellina solita!!!
![]() Aggiungendo e togliendo alla medie campionarie 1,96 errori standard,
Aggiungendo e togliendo alla medie campionarie 1,96 errori standard,
Questo
vuol dire che se c’è un altro ricercatore che ripete il mio esperimento, ho il 95% di probabilità che la media a lui risulti compresa in quei limiti, ma rimane sempre una probabilità su 20 che gli venga un valore diverso: con un 5% di probabilità di aver sbagliato tutto!Nel campo delle stime, c’è l’errore standard che è il migliore indicatore di precisione della media stimata per campionamento.
L’errore dipende dalla variabilità del campione, dalla sua numerosità (più è grande il campione più è preciso). N.B.: questo vale anche per dati qualitativi:
Esempio:
Universo di 100000 persone di cui 60000 donne e 40000 uomini.
Facendo dei campionamenti casuali da 1000 persone puo' venir fuori:
Ecc. ecc.
Bernoulli calcolò tutti i campioncini di un universo del genere e trovò che mettendo su un asse cartesiano le frequenze relative di maschi, otteneva una curva di Gauss.
"Per i fenomeni binomiali quando la frequenza di un evento è compresa tra il 10% e il 90% (fenomeni comuni) e quando il campione è molto numeroso la stima per campionamento segue la legge di Gauss".
Si procede allora per analogia:
Tendenza centrale = frequenza relativa
e.s. = ![]()
(dove n è la numerosità del campione, P è la proporzione di maschi o comunque dell'evento che mi interessa studiare)
Visto come assomigia l'
errore standard per i dati qualitativi all' indice di eterogeneità di Gini ?Per il campionamento di dati qualitativi si può fare una stima della tendenza centrale ad un livello di probabilità accettabile.
|
Limiti di confidenza della distribuzione di proporzioni campionarie |
% di possibili proporzioni campionarie comprese |
Probabilità che la frequenza universale(sconosciuta) cada entro i limiti indicati dalla prima colonna |
|
p + 0,67 |
50% |
0,5 |
|
p — 0,67 |
||
|
p + 1 |
68,3% |
0,683 |
|
p - 1 |
||
|
p + 1,96 |
95% |
0,95 |
|
p — 1,96 |
||
|
p + 2 |
95,5% |
0,955 |
|
p — 2 |
||
|
p + 2,57 |
99% |
0,99 |
|
p — 2,57 |
||
|
p + 3 |
99,7% |
0,997 |
|
p - 3 |
E lo stesso per i dati quantitativi:
|
Limiti di confidenza della distribuzione di medie campionarie |
% di possibili medie campionarie comprese |
Probabilità che la media universale(sconosciuta) cada entro i limiti indicati dalla prima colonna |
|
M + 0,67 e.s. |
50% |
0,5 |
|
M — 0,67 e.s. |
||
|
M + 1 e.s. |
68,3% |
0,683 |
|
M - 1 e.s. |
||
|
M + 1,96 e.s. |
95% |
0,95 |
|
M — 1,96 e.s. |
||
|
M + 2 e.s. |
95,5% |
0,955 |
|
M — 2 e.s. |
||
|
M + 2,57 e.s. |
99% |
0,99 |
|
M — 2,57 e.s. |
||
|
M + 3 e.s. |
99,7% |
0,997 |
|
M - 3 e.s. |
14/12/2001
Possiamo distinguere una statistica descrittiva e una inferenziale.
La statistica inferenziale studia
CI VUOLE TANTA CAUTELA!!! Vedete questo esempio:
Su 50 pazienti che si presentano con piaghe da decubito,
abbiamo provato due diversi disinfettanti.
L'assegnazione è stata fatta in base all'arrivo in reparto con
randomizzazione ristretta
|
DISINFETTANTE |
X |
DISINFETTANTE |
Y |
|
Evento |
Tempo |
Evento |
Tempo |
|
Guarito |
10 |
Guarito |
2 |
|
Dimesso con piaga |
12 |
Guarito |
4 |
|
Guarito |
15 |
Guarito |
5 |
|
Guarito |
13 |
Guarito |
6 |
|
Guarito |
14 |
Guarito |
7 |
|
Ancora con piaga a fine periodo |
18 |
Dimesso con piaga |
8 |
|
Ancora con piaga a fine periodo |
22 |
Ancora con piaga a fine periodo |
9 |
|
Ancora con piaga a fine periodo |
23 |
Ancora con piaga a fine periodo |
10 |
|
Dimesso con piaga |
25 |
Ancora con piaga a fine periodo |
8 |
|
Guarito |
12 |
Ancora con piaga a fine periodo |
10 |
|
Guarito |
15 |
Ancora con piaga a fine periodo |
8 |
|
Dimesso con piaga |
19 |
Ancora con piaga a fine periodo |
3 |
|
Guarito |
14 |
Fuggito con la capo-sala |
7 |
|
Guarito |
12 |
Guarito |
5 |
|
Guarito |
11 |
Guarito |
6 |
|
Ancora con piaga a fine periodo |
19 |
Ancora con piaga a fine periodo |
8 |
|
Ancora con piaga a fine periodo |
12 |
Dimesso con piaga |
1 |
|
Ancora con piaga a fine periodo |
14 |
Guarito |
5 |
|
Ancora con piaga a fine periodo |
15 |
Dimesso con piaga |
6 |
|
Guarito |
15 |
Guarito |
9 |
|
Ancora con piaga a fine periodo |
11 |
Ancora con piaga a fine periodo |
8 |
|
Guarito |
13 |
Ancora con piaga a fine periodo |
8 |
|
Dimesso con piaga |
7 |
guarito |
14 |
|
Ancora con piaga a fine periodo |
16 |
Ancora con piaga a fine periodo |
17 |
|
Guarito |
25 |
||
|
Ancora con piaga a fine periodo |
7 |
Come facciamo? Eliminiamo quelli di cui non conosciamo l'esito finale perché dimessi o fuggiti con la caposala?
|
DISINFETTANTE |
X |
DISINFETTANTE |
Y |
|
Evento |
Tempo |
Evento |
Tempo |
|
Guarito |
10 |
Guarito |
2 |
|
Guarito |
4 |
||
|
Guarito |
15 |
Guarito |
5 |
|
Guarito |
13 |
Guarito |
6 |
|
Guarito |
14 |
Guarito |
7 |
|
Ancora con piaga a fine periodo |
18 |
||
|
Ancora con piaga a fine periodo |
22 |
Ancora con piaga a fine periodo |
9 |
|
Ancora con piaga a fine periodo |
23 |
Ancora con piaga a fine periodo |
10 |
|
Ancora con piaga a fine periodo |
8 |
||
|
Guarito |
12 |
Ancora con piaga a fine periodo |
10 |
|
Guarito |
15 |
Ancora con piaga a fine periodo |
8 |
|
19 |
Ancora con piaga a fine periodo |
3 |
|
|
Guarito |
14 |
||
|
Guarito |
12 |
Guarito |
5 |
|
Guarito |
11 |
Guarito |
6 |
|
Ancora con piaga a fine periodo |
19 |
Ancora con piaga a fine periodo |
8 |
|
Ancora con piaga a fine periodo |
12 |
||
|
Ancora con piaga a fine periodo |
14 |
Guarito |
5 |
|
Ancora con piaga a fine periodo |
15 |
||
|
Guarito |
15 |
Guarito |
9 |
|
Ancora con piaga a fine periodo |
11 |
Ancora con piaga a fine periodo |
8 |
|
Guarito |
13 |
Ancora con piaga a fine periodo |
8 |
|
guarito |
14 |
||
|
Ancora con piaga a fine periodo |
16 |
Ancora con piaga a fine periodo |
17 |
|
Guarito |
25 |
||
|
Ancora con piaga a fine periodo |
7 |
Ci focalizziamo solo sui tempi di guarigione?
|
TRATTAMENTO |
N |
media |
Deviazione standard |
Errore standard |
|
Disinfettante X |
12 |
14,08 |
3,80 |
1,10 |
|
Disinfettante y |
10 |
6,30 |
3,27 |
1,03 |
T di student per dati non appaiati
|
Valore di t |
Significatività (2-code) |
Differenza delle medie |
|
5,091 |
,000 |
7,78 |
|
Errore standard di tale differenza |
95% Confidence Interval di tale differenza |
95% Confidence Interval di tale differenza |
|
Lower (inferiore) |
Upper (superiore) |
|
|
1,53 |
4,59 |
10,97 |
Il disinfettante y è una bomba!!!!
Ci focalizziamo solo sugli esiti: guarito o non guarito?
|
ESITO |
Total |
||
|
|
non guarito |
guarito |
|
|
disinfettante x |
10 |
12 |
22 |
|
disinfettante y |
10 |
10 |
20 |
|
totale |
20 |
22 |
42 |
Chi-Square Tests
|
Valore del chi square |
Gradi di libertà |
Significatività (2-code |
|
|
Pearson Chi-Square |
,087 |
1 |
,768 |
|
N of Valid Cases |
42 |
Il disinfettante y è assolutamente uguale all'altro!!!!
Test per verificare la differenza statistica delle due curve di sopravvivenza con i due diversi disinfettanti
|
Valore |
Gradi di libertà |
Significatività |
|
|
Log Rank |
9,22 |
1 |
,0024 |
|
Breslow |
11,57 |
1 |
,0007 |
|
Tarone-Ware |
10,83 |
1 |
,0010 |
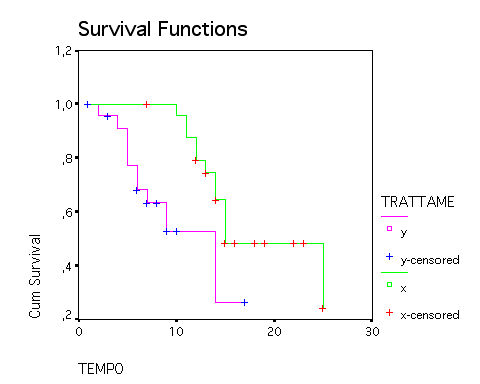
Il disinfettante y è efficace più in fretta dell'altro, ma non fa guarire più gente: questa è la verità salvo errrore 0,05. Qui si è usato il test giusto!!!!
Trial
= studio nel corso del quale seguo nel tempo due (o +) gruppi di pazienti trattati con farmaci diversi. Sono uomini, non cavie da esperimento, quindi a volte non si ripresentano ai ocntrolli!!!Gli esiti, in questo caso, saranno guariti, non guariti e altri che vengono dimessi prima o di cui non si sa più nulla, persone che non posso eliminare.Se lo facessis, perderei informazioni e otterrei risultati falsi
Eliminando questi ultimi, pur perdendo delle informazioni, calcolo i tempi di guarigione tra quelli guariti e quelli no.
Per ottenere un intervallo di confidenza al 95% bisogna moltiplicare l’errore standard per +/- 1,96.
La stima puntuale è limitata a un valore, mentre la stima intervallare è quella che attorno alla media prende i valori pari a circa 2 errore standard.
Se la probabilità che la differenza sia dovuta al campionamento è alta, allora i disinfettanti sono uguali, mentre se la probabilità è bassa, i disinfettanti, allora, sono differenti.
Si ha differenza statisticamente significativa, quando la probabilità che tale differenza sia dovuta soltanto al campionamento o al caso è inferiore a 0,05 (5%)
Sono importanti il livello di confidenza e l’idoneità del test al caso specifico.
Il CINAHL è la banca dati degli infermieri
Cumulative
Index to
Nursing and
Allied
Health
Literature
http://www.yale.eduCinahl Information Systems
Customer Service Department
1509 Wilson Terrace
Glendale, CA 91206
Hours: Monday through Friday, 8:00 a.m. to 5:00 p.m. PST
Tel: 818-409-8005, ext. 5341
Fax: 818-546-5679
E-mail:
support@cinahl.com
21/12/2001
Altrettanta attenzione occorre con i test di correlazione:
Vogliamo verificare la qualità percepita, cioè al fatto che i pazienti si sentano seguiti nel modo più corretto.
Per verificare come vanno le cose vengono distribuiti dei questionari anonimi al termine del ricovero, con domande sulla gentilezza, prontezza, accuratezza del lavoro del personale.
Il questionario in uso ha un punteggio che puo' variare
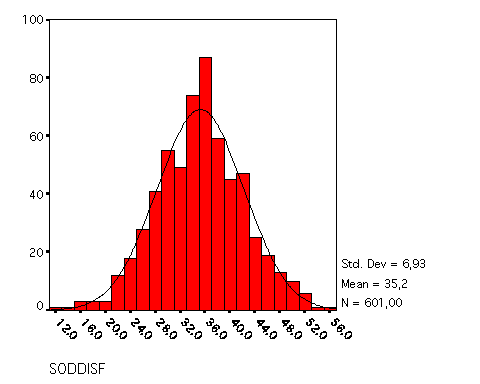
Questi sono i risultati di 601 questionari.
Il 20% dei pazienti ha un punteggio <30, cioè è scontento. Come mai?
Dipenderà dal fatto che gli infermieri non hanno studiato a dovere la statistica?
Apparentemente, purtroppo, no
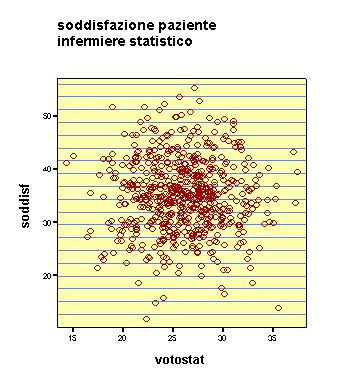
Dipenderà dal fatto che gli infermieri fanno troppi straordinari?
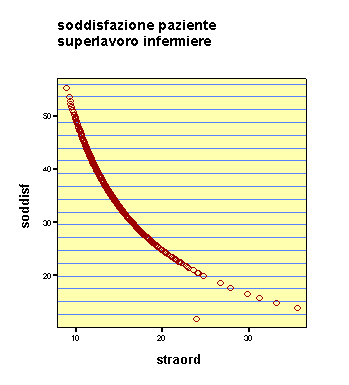
C'è solo un puntino di coordinate 25, 11 che deve esser proprio un somarone: lavora poco e fa scontenti gli utenti!
Dipenderà dal fatto che gli infermieri guadagnano troppo?
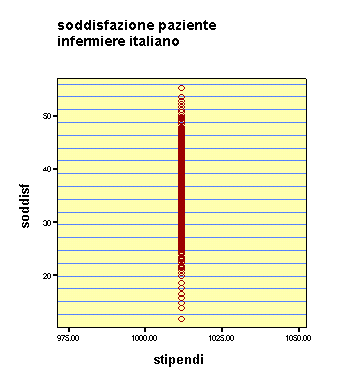
Queste le immaini grafiche. Anche il risultato delle formule, conferma le impressioni:
|
SODDISF |
|
|
SODDISF |
1,000 |
|
Sig. |
, |
|
STRAORD |
-,946 |
|
Sig. |
,000 |
|
VOTOSTAT |
-,004 |
|
Sig. |
,927 |
|
STIPENDI |
, |
|
Sig. |
, |
** Correlation is significant at the 0.01 level (2-tailed).
a Cannot be computed because at least one of the variables is constant.
Ci sono anche modi più "istintivi" di fare statistica, ma non meno pericolosi:
Tra le prime 250 donne visitate nel servizio di oncologia, tutte in menopausa, ci accorgiamo che:
su 14 donne in menopausa
operate di K mammario
Brune 10/14
Bionde 4/14
Tra le paz. con K mammario, il 71,5% sono brune e il 28,5 sono bionde??? Grande scoperta!
NON FIDIAMOCI DI QUESTI CALCOLINI E CHIEDIAMO IL TEST ADATTO:
|
Value |
95% Confidence |
Interval |
|
|
|
Lower |
Upper |
|
|
Odds Ratio for colore |
2,963 |
0,904 |
9,715 |
|
N of Valid Cases |
250 |
IL COLORE BRUNO SAREBBE UN FATTORE DI RISCHIO SE L'ODDS RATIO FOSSE >1. Nel limite di confidenza inferiore, non lo è, nel limite di confidenza superiore lo è. Questa "scoperta" la buttiamo nel cestino!
Tra le prime 250 donne visitate nel servizio di oncologia, tutte in menopausa, ci accorgiamo che:
su 14 donne in menopausa
malate di K mammario
Obese 10/14
Non obese 4/14
Tra le paz. con K mammario, il 71,5% sono obese e il 28,5 non sono obese??? Grande scoperta!
NON FIDIAMOCI DI QUESTI CALCOLINI E CHIEDIAMO IL TEST ADATTO:
|
Value |
95% Confidence |
Interval |
|
|
|
Lower |
Upper |
|
|
Odds Ratio for OBESE |
4,056 |
1,235 |
13,316 |
|
N of Valid Cases |
250 |
SICCOME Odds ratio >1 sia nel limite di confidenza inferiore che nel superiore, mi resta il dubbio che l'obesità in menopausa faciliti il K mammario (in effetti è così).