

Il test di Kolmogorov-Smirnov si applica a distribuzioni
continue ponendo a confronto la distribuzione cumulativa teorica
con la distribuzione cumulativa osservata.
Il test si basa sulla differenza D che rappresenta
la differenza massima, in valore assoluto, tra le due
distribuzioni cumulative ed è definita come segue:
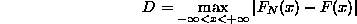
dove F(x)è la funzione di distribuzione cumulativa
teorica e FN(x) è la funzione di distribuzione
cumulativa campionaria.
Se x1, x2, ..., xN
è un campione casuale, FN(x) rappresenta il
numero (rapportato ad N) degli elementi del campione xi,
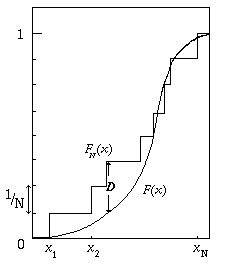
minori od uguali ad x. Nella figura che segue sono
rappresentate la F(x) e la FN(x): si
vede che, da come è stata definita, FN(x) è
costante tra xi e xi+1
e ogni gradino è pari ad 1/N.
Per esempio, se il campione è costituito da una successione
di ui, con i compreso tra
1 ed N, si calcola il valore assoluto della differenza D
tra la funzione di distribuzione cumulativa FN(u)
e la funzione di distribuzione cumulativa della variabile casuale
U, uniformemente distribuita in (0,1). Analogamente
al caso del test del chi-quadrato, D viene
confrontato con certi valori critici Da
(ad esempio a=0.01 o a=0.05) per decidere se
accettare o meno l'ipotesi che i numeri ui
siano equamente distribuiti.
A differenza del test del chi-quadrato, il test di Kolmogorov e
Smirnov offre il vantaggio di non richiedere che i dati siano in
qualche modo raggruppati e, quindi, non dipende da come vengono
scelte le categorie nelle quali ripartire la sequenza.