In questa sezione affronteremo il problema di come combinare
due o più misure indipendenti di una singola grandezza fisica.
Capita infatti che molto spesso una grandezza fisica venga
misurata parecchie volte, magari anche in laboratori differenti:
in questo modo sorge il problema di come combinare queste misure
per ottenere una singola stima.
Supponiamo di avere le seguenti due misure di una grandezza fisica:
Prima misura: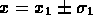 
Seconda misura: 
Supponendo che la discrepanza tra la due misure non sia tale
da doverle considerare inconsistenti e quindi sospettare che una
delle due sia errata: ci chiediamo come valutare la miglior stima
della grandezza x basandoci sulle due misure a nostra
disposizione.
Se le due incertezze 
e 
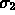non sono uguali dobbiamo procedere in
un altro modo in quanto la semplice media aritmetica darebbe la
medesima importanza ad entrambe le misure, mentre bisognerebbe in
qualche modo attribuire alla misura più precisa un'importanza
(un "peso") maggiore.
Si definiscono i pesi (w) delle diverse misure come l'inverso dei quadrati delle incertezze corrispondenti:
Attraverso questa definizione si intuisce facilmente come una
misura più precisa abbia maggior peso rispetto alle altre.
Da questa definizione discende quella di media pesata
come:
Quale sarà ora l'errore da associare al risultato così ottenuto?
Nota
La
media