|
Alcune considerazioni sugli erroriL'incertezza indicata nella colonna di destra del
Questo errore è solo indicativo. Di solito notiamo che, per quanto accurata sia la misurazione, in seguito ad alcune prove con i nostri semplici strumenti si ottiene un errore maggiore di quello calcolato teoricamente. Ciò è dovuto al fatto che non sono pochi i fattori "di disturbo" in varie fasi dell'operazione: piccoli ma sensibili scostamenti dalla verticalità dello gnomone o dall'orizzontalità del piano su cui si proietta l'ombra (o del foglio di carta appoggiato sul banco), difficoltà nel determinare la posizione esatta dell'estremità dell'ombra, errori di parallasse nella lettura ecc. Possiamo notare inoltre che, a parità di strumento usato per misurare le lunghezze, la precisione aumenta con l'aumentare dell'altezza dello gnomone (e, di conseguenza, della lunghezza dell'ombra). La tabella seguente ci offre un esempio:
Considerando l'incertezza di un millimetro per entrambe le misure, dimezzando e triplicando h e b, l'errore si riduce rispettivamente a un mezzo e a un terzo. Purtroppo nel nostro caso pratico, ciò
non è del tutto valido: aumentando la lunghezza dell'ombra aumenta
anche un fattore di disturbo notevole: le ombre divengono meno nitide
per l'aumento dei bordi di
|
|
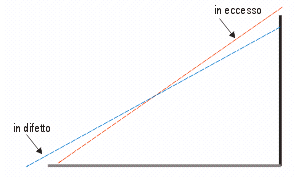 come
si vede in figura, esse sono date da 1) una misura troppo grande
dell'altezza dello gnomone combinata con una misura troppo piccola della
lunghezza dell'ombra (l'angolo alfa risulta in eccesso - tratteggio
in rosso) oppure da 2) una misura troppo piccola per lo
come
si vede in figura, esse sono date da 1) una misura troppo grande
dell'altezza dello gnomone combinata con una misura troppo piccola della
lunghezza dell'ombra (l'angolo alfa risulta in eccesso - tratteggio
in rosso) oppure da 2) una misura troppo piccola per lo