


- Siano a e b vettori di modulo rispettivamente 3
e 5. Le rette direttrici dei due vettori formano un angolo di
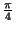 .
Calcolare il p.s. (prodotto scalare) di a
.
Calcolare il p.s. (prodotto scalare) di a b.
b.
- Siano a e b vettori di componenti cartesiane (3,7,1)
e (-1,6,0). Calcolare il seno dell'angolo compreso tra loro.
- Dimostrare il teorema di Carnot.
- Determinare il valore del parametro y per cui i due vettori
a e b sono ortogonali. a=30i+2yj-k
e b =i+7j+yk
- Dimostrare che i vettori (a + b) e (a
- b) sono ortogonali solo se a e b hanno
lo stesso modulo.
- Siano r una retta nello spazio, b un vettore orientato
lungo r e a un vettore qualunque. Esprimere la proiezione
di a sulla retta r.
- Siano a=12i+4k e b=5j-8k.
Calcolare axb e rappresentarlo graficamente nel
sistema di riferimento i,j,k.
- Trovare un versore contemporaneamente ortogonale ai 2 vettori a,b
precedenti.
- Siano a=3i+3j-2k, b =i+7j+k,
c=5i-k. Sono complanari? Motivare la risposta.
- Il segno del prodotto misto di 3 vettori come cambia se si esegue
uno scambio di due vettori? E con due scambi?
-
Calcolare
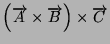
e
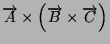
- Ricavare i valori di
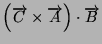 ,
,
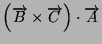 e
e
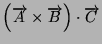 impiegando i vettori precedenti.
impiegando i vettori precedenti.
- Dati i tre vettori
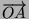 ,
,
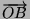 ,
,
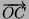 , tracciati sul piano cartesiano (fig.1),
determinare:
, tracciati sul piano cartesiano (fig.1),
determinare:
il valore dell'angolo 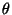 , angolo intercettato
dal segmento
, angolo intercettato
dal segmento 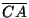 e dal segmento
e dal segmento 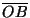 ;
;
di nuovo il valore di 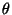 dopo aver spostato il punto C nelle
coordinate (1,5).
dopo aver spostato il punto C nelle
coordinate (1,5).
- Supponendo di conoscere due vettori b,c giacenti sul piano
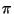 , si calcoli la proiezione di un vettore a su di una
retta ortogonale al piano stesso.
, si calcoli la proiezione di un vettore a su di una
retta ortogonale al piano stesso.
- Dati i seguenti tre vettori, con {i, j, k}
base ortonormale in
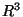 :
:
calcolare il vettore risultante
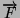 ed esprimerlo
in forma cartesiana ed in coordinate polari;
ed esprimerlo
in forma cartesiana ed in coordinate polari;
calcolare il volume
del parallelepipedo avente per spigoli i tre vettori
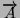 ,
,
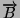 ,
,
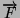 ;
;
determinare il prodotto
scalare di
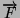 con il vettore
con il vettore
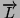 definito in coordinate cilindriche:
definito in coordinate cilindriche: 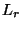 =3;
=3; 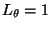 radiante;
radiante;
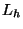 = -1.
= -1.
- Nello spazio euclideo sono dati tre punti Q(5,10,1) W(1,0,6) E(-4,-5,2).
Determinare l'area del triangolo di cui Q, W ed E rappresentano i
vertici.
- Prendiamo un cubo di lato l e sia
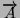 la diagonale
di una faccia. Calcolare l'angolo compreso tra il vettore
la diagonale
di una faccia. Calcolare l'angolo compreso tra il vettore
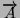 e la diagonale principale del solido.
e la diagonale principale del solido.
- Dimostrare che una qualunque rotazione di un vettore
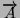 intorno all'asse z si ottiene
intorno all'asse z si ottiene
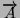 '=R(
'=R(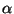 )
)
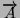 con R(
con R(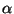 )=
)=
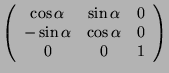
- Data la relazione
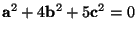 determinare
la risultante dei tre vettori a,b,c.
determinare
la risultante dei tre vettori a,b,c.
- Siano quattro vettori a,b,c,d , tali che:
con moduli rispettivamente a=18, b=23, c=27, d=11. Si determini
i valori massimo e minimo che puó assumere 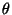 angolo compreso
tra a e b.
angolo compreso
tra a e b.
- Sia L un vettore di componenti cartesiane parametriche:
calcolarne la derivata parziale prima rispetto al parametro c
e al parametro t. Determinare inoltre il valore dell'integrale
di L calcolato in funzione di t.
- Sia un vettore a disposto in un piano. Il vettore presenta
un modulo a
ed un angolo 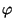 compreso tra la direttrice di
compreso tra la direttrice di
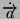 e l'asse delle ascisse pari a
e l'asse delle ascisse pari a
Determinare il modulo della velocitá all'istante t=3s sapendo
che g=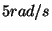 e c=2
e c=2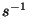
- Premessa: Siano F un vettore e P il suo punto d'applicazione.
Si definisce momento di F rispetto al punto O il vettore
M tale che:
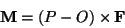 |
(1) |
Si puó pure definire la proiezione del momento M su di una
qualunque retta orientata passante per il punto O come momento assiale
di F:
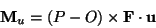 |
(2) |
Due sistemi di vettori si dicono equivalenti se hanno uguali sia la
risultante sia il momento risultante1.
Esercizio: Siano tre vettori
applicati rispettivamente nei punti
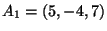 ,
,
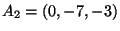 ,
,
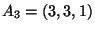 . Determinare la risultante e il momento risultante
calcolato scegliendo O nell'origine degli assi. In seguito prendere
O nel punto (3,3,1).
. Determinare la risultante e il momento risultante
calcolato scegliendo O nell'origine degli assi. In seguito prendere
O nel punto (3,3,1).
This document was generated using the
LaTeX2HTML translator Version 2002 (1.62)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -no_subdir -split 0 -show_section_numbers /tmp/lyx_tmpdir3222FOMJtr/lyx_tmpbuf1/exx1.tex
The translation was initiated by gabriele on 2004-01-25
Footnotes
- ... risultante1
- Queste definizioni torneranno utili nella statica e nei sistemi rotanti,
argomenti che verranno descritti successivamente.



gabriele
2004-01-25
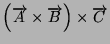 e
e
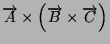
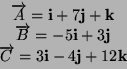
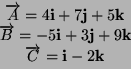
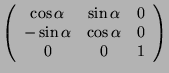
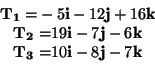
![\includegraphics[]{/tmp/lyx_tmpdir3222FOMJtr/lyx_tmpbuf1/_home_balbi_oggi_24_01_algebra_Vettoriale_eser_es1}](img15.png)