

- Dati i vettori a,b il loro prodotto scalare é dato da:
- Per prima cosa vanno determinati i moduli dei due vettori:
Ora calcolo il prodotto scalare dei due vettori:
ricordo che
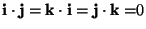 segue dunque che
segue dunque che
- Dati i tre vettori a,b,c con c=a-b. Elevando al
quadrato la relazione ottengo:
ovvero
C.V.D.
- Per risolvere quest'esercizio basta imporre che il prodotto scalare
dei due vettori sia zero:
- Per quanto visto negli esercizi precedenti segue che:
C.V.D.
- L'applicazione di un prodotto scalare é proprio una proiezione lungo
un asse, per cui:
cioé trovo un versore che giace su r sul quale proiettare a.
Questa é una proprietá utilissima. Esprimere un vettore nelle sue
componenti cartesiane significa proiettarlo sui tre assi del sistema
di riferimento ortogonale xyz, ovvero significa fare il prodotto scalare
del vettore con i tre versori i,j,k.
- Il metodo piú veloce per calcolare un prodotto vettoriale é quello
del determinante:
- Molto semplicemente si tratta di trasformare il vettore trovato prima
in un versore. Bisogna dividerlo per la sua stessa norma:
- Per prima cosa bisogna trovare il prodotto vettoriale di una coppia
dei vettori. Il prodotto vettore ottenuto é ortogonale al piano individuato
dai primi due vettori. Per vedere se il terzo vettore é complanare
agli altri basta verificare se non ha alcuna proiezione sul prodotto
vettore:
per questo motivo i tre vettori non giacciono sullo stesso piano.
Il valore numerico che é stato trovato é in realtá il volume del solido
avente per spigoli i tre vettori. Se i tre vettori fossero stati tutti
sullo stesso piano avremmo avuto un parallelepipedo degenere (schiacciato
sul piano) di volume zero.
- Come abbiamo calcolato nell'esercizio precedente
il prodotto misto vale:
Se scambio a con b ottengo un'inversione di segno
per le note proprietá. Un modo compatto e pratico per vedere e calcolare
un prodotto misto é il determinante del tipo:
in questa rappresentazione, scambiare due vettori significa scambiare
due righe. Supponiamo di scambiare a con c:
mentre se fosse stato calcolato nella forma originale avremmo ottenuto:
cioé l'opposto. Continuando si puó mostrare che ad uno scambio corrisponde
un cambio di segno nel prodotto misto. Due scambi mantengono il segno
inalterato:
- I risultati:
- Per quanto detto al punto 10 si puó notare che
scelto uno dei tre prodotti, gli altri possono essere ottenuti realizzando
due scambi di vettori. Per questo motivo calcolato uno, gli altri
sono identici anche di segno: 467.
- Come dovrebbe essere noto, i vettori, dal punto di vista geometrico
sono frecce orientate. Pertanto dal disegno fornito possiamo determinare
tutti gli elementi di partenza. Il punto C ha inizialmente coordinate
C(1,2), mentre A e B sono A(5,2) e B(3,4). I tre vettori che consideriamo
partono tutto dal punto O(0,0), pertanto le coordinate dei punti A,B,C
forniscono immediatamente le componenti cartesiane dei vettori. A=5i+2j,
B=3i+4j, C=i+2j. Il
segmento CA non é altro che il vettore differenza tra OA e OC. Il
prodotto scalare tra CA e OB garantisce l'informazione sull'angolo
compreso:
I piú attenti avranno notato che non era necessario fare tutti questi
conti. Infatti il segmento CA é parallelo all'asse delle ascisse,
quindi il coseno dell'angolo cercato non é altro che
Se si sposta il punto C, allora si rendono necessari tutti i calcoli
precedenti:
come era giusto attendersi dalla figura.
- La direzione della retta ortogonale al piano puó essere determinata
eseguendo il prodotto vettore tra i b,c. Si determina il
versore e si proietta a lungo la retta:
- La somma vettoriale dei tre vettori, calcolabile pure attraverso il
metodo della poligonale1, vale:
Per rappresentare questo vettore in coordinate polari, basta semplicemente
calcolare il valore 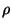 , e di seguito ricavare i valori dei due
angoli:
, e di seguito ricavare i valori dei due
angoli:
segue che
 in coordinate polari. Per calcolare il volume del solido, il procedimento
é noto per cui:
in coordinate polari. Per calcolare il volume del solido, il procedimento
é noto per cui:
Infine conviene trasformare in coordinate cartesiane il vettore L:
- Prendo i due vettori (segmenti orientati) QW e EW:
segue che l'area del triangolo vale:
- Come mostra la figura 1, possiamo considerare la diagonale
della faccia del cubo dal punto O al punto
 (l,l,0); mentre
come diagonale principale prendiamo quella del punto
(l,l,0); mentre
come diagonale principale prendiamo quella del punto 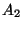 (l,l,l).
Segue che
(l,l,l).
Segue che
- Per risolvere questo esercizio é sufficiente fare qualche considerazione
geometrica. L'operazione di rotazione é una trasformazione che puó
essere condensata in una matrice 3x3. Data una terna di assi di partenza
(x,y,z) si ottiene una nuova terna (x',y',z').
Figure 2:
Rotazione di un sistema di riferimento.
|
|
La figura 2 mostra che i nuovi assi X' e Y' sono
esprimibili come una combinazione lineare dei due vecchi assi X e
Y:
Segue facilmente che la matrice che realizza questa trasformazione
é proprio quella dell'esercizio.
- Le norme sono, per definizione, tutte positive quindi a,b,c
sono identicamente nulli.
- Prendo l'equivalenza enunciata nel testo e l'elevo al quadrato:
segue che
- Ecco le derivate parziali:
- Per prima cosa determiniamo le proiezioni del vettore a sugli
assi cartesiani e poi deriviamo rispetto al tempo:
e dunque il modulo vale:
per cui il coseno dell'angolo compreso tra
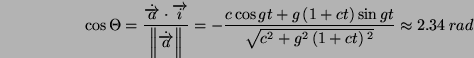 e l'asse delle ascisse vale:
e l'asse delle ascisse vale:
mentre il modulo all'istante t=3s é:
- La risultante somma vale:
mentre il momento delle forze calcolato rispetto al punto O (0,0,0):
Prendendo come punto di riduzione il punto (3,3,1) si ottiene:
This document was generated using the
LaTeX2HTML translator Version 2002 (1.62)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -no_subdir -split 0 -show_section_numbers /tmp/lyx_tmpdir32278CZJug/lyx_tmpbuf0/risolv3.tex
The translation was initiated by gabriele on 2004-02-07
Footnotes
- ... poligonale1
- Questo metodo di calcolo geometrico é molto utile negli esercizi di
statica.


gabriele
2004-02-07

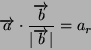

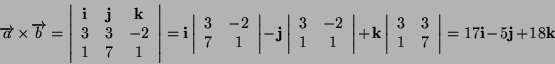
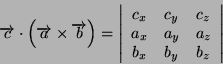
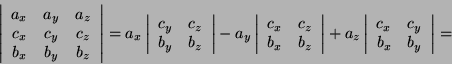
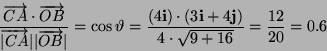
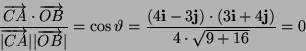
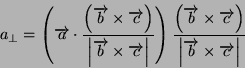
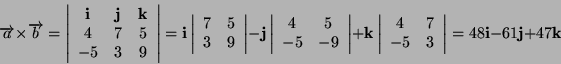
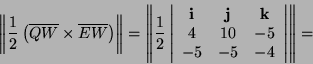
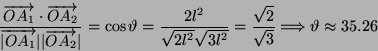
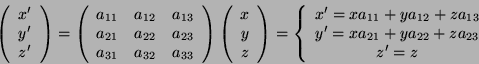
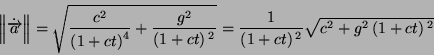
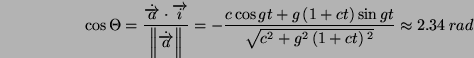 e l'asse delle ascisse vale:
e l'asse delle ascisse vale:
