

- Si tratta di applicare la nozione di prodotto scalare.
- Versione leggermente modificata del punto precedente.
- Ricordare come si realizza una differenza di vettori ed elevare ...
- Due vettori sono ortogonali se il coseno dell'angolo compreso ...
- Anche qui si tratta di applicare la classica definizione di prodotto
scalare tra i due vettori (a-b) e (a+b).
- Un'altra applicazione del prodotto scalare.
- Il prodotto vettoriale assume una forma molto semplice se si applica la
rappresentazione con i determinanti.
- Un altro aspetto del prodotto vettore.
- Si tratta di vericare se il prodotto vettore axb é
ortogonale a c.
- Provare per credere.
- Si tratta di reiterare l'operazione di determinante piú volte.
- Altro esercizio simile ai precedenti.
- Differenza di vettori e prodotto scalare per trovare l'angolo
compreso.
- Se i due vettori b,c non sono collineari allora posso trovare un
versore ortogonale su cui proiettare a...
- Ricordo che le coordinate polari valgono:
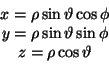 |
(1) |
quindi non é altro che un sistema da ¨rovesciare¨ per trovare la forma
polare di F (
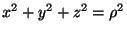 , ecc.). Il primo passo per calcolare
il volume é determinare l'area di base del solido. Infine per realizzare
il prodotto scalare é conveniente passare alle coordinate cartesiane.
, ecc.). Il primo passo per calcolare
il volume é determinare l'area di base del solido. Infine per realizzare
il prodotto scalare é conveniente passare alle coordinate cartesiane.
- Questo esercizio si risolve ragionando come abbiamo fatto al punto
precedente.
- Ancora un'applicazione del prodotto scalare...
- Si puó partire considerando una base vettoriale che viene fatta ruotare
di un angolo a ottenendo cosí una nuova base.
- Ricordarsi che della definizione di combinazione linearmente
indipendente...
- Basta sviluppare applicando la definizione di prodotto scalare.
- Mera applicazione delle definizioni.
- Conviene esprimere prima le componenti cartesiane del vettore
a.
- Seguire le istruzioni.
This document was generated using the LaTeX2HTML
translator Version 2002 (1.62)
Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer
Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics
Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -no_subdir -split 0 -show_section_numbers
/tmp/lyx_tmpdir9893U9NR3c/lyx_tmpbuf2/solves1.tex
The translation was initiated by root on 2004-01-08


root 2004-01-08