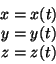

La posizione istantanea P(t) di un punto materiale lungo una qualunque
traiettoria puó essere individuata in maniera univoca da un vettore
r(t). Inizialmente si stabilisce un sistema di riferimento di
coordinate e dal suo centro si traccia il vettore posizione 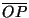 .
Se l'oggetto é in moto allora senz'altro é individuabile una variazione del
vettore r(t) e quindi é possibile definire quella che viene chiamata
velocitá istantanea.
.
Se l'oggetto é in moto allora senz'altro é individuabile una variazione del
vettore r(t) e quindi é possibile definire quella che viene chiamata
velocitá istantanea.
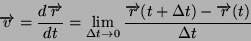 |
(1) |
ove il vettore
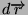 é chiamato vettore spostamento. Se il
vettore posizione é espresso in coordinate cartesiane, allora la velocitá
istantanea vale:
é chiamato vettore spostamento. Se il
vettore posizione é espresso in coordinate cartesiane, allora la velocitá
istantanea vale:
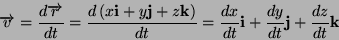 |
(2) |
il cui modulo vale
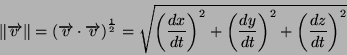 |
(3) |
Questa quantitá é la lunghezza d'arco che in un istante 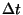 viene
percorso dal punto materiale. Esiste anche la definizione di velocitá
media espressa da:
viene
percorso dal punto materiale. Esiste anche la definizione di velocitá
media espressa da:
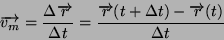 |
(4) |
Soffermiamoci ancora sulle eq.(2), (3). Essenzialmente abbiamo inteso indicare
il punto P=P(t) con componenti:
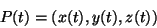 |
(5) |
Le tre equazioni
rappresentano il luogo geometrico dei punti occupati nel tempo da P e
costituiscono perció l'equazione della traiettoria del punto materiale.
Talvolta é di grande utilitá fissare un sistema di riferimento ortogonale
solidale al punto materiale in movimento. Determinata la traiettoria si
indica la posizione su di essa del punto P mediante l'equazione oraria del
moto:
con cui posso scrivere:
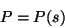 |
(6) |
Nella sostanza l'eq 6 non esprime concetti
differenti dalla eq. 5 in quanto l'ascissa
curvilinea s é funzione del tempo. Se vogliamo esprimere la velocitá
in termini di ascisse curvilinee allora:
Il versore  , definito come
, definito come 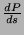 ,
é in ogni punto tangente alla curva ed diretto nel senso delle s crescenti se
,
é in ogni punto tangente alla curva ed diretto nel senso delle s crescenti se
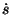 é positivo (moto progressivo), mentre nel caso di moto
retrogrado, il valore
é positivo (moto progressivo), mentre nel caso di moto
retrogrado, il valore 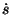 é negativo. Da questo versore é poi
possibile ricavare altri due vettori di modulo unitario tra loro ortogonali
in maniera da completare una terna di assi cartesiani solidale al punto
materiale. Nella letteratura, generalmente, sono indicati come versori
é negativo. Da questo versore é poi
possibile ricavare altri due vettori di modulo unitario tra loro ortogonali
in maniera da completare una terna di assi cartesiani solidale al punto
materiale. Nella letteratura, generalmente, sono indicati come versori
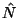 (normale) e
(normale) e 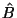 (binormale).
Per determinare il versore
(binormale).
Per determinare il versore 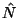 dobbiamo dimostrare che
dobbiamo dimostrare che
 é perpendicolare a
é perpendicolare a  . Si parte
osservando che il prodotto scalare
. Si parte
osservando che il prodotto scalare
 per cui posso scrivere:
per cui posso scrivere:
il che dimostra che
 é normale a
é normale a  . Segue che:
. Segue che:
con k=1/R (R=raggio di curvatura). Evidentemente k é il modulo di
 . Infine il versore binormale
. Infine il versore binormale 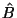 ottiene con
ottiene con
This document was generated using the LaTeX2HTML
translator Version 2002 (1.62)
Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer
Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics
Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -no_subdir -split 0 -show_section_numbers
/tmp/lyx_tmpdir2830n92mNp/lyx_tmpbuf0/intrcine2.tex
The translation was initiated by gabriele on 2004-02-05


gabriele 2004-02-05
![]() .
Se l'oggetto é in moto allora senz'altro é individuabile una variazione del
vettore r(t) e quindi é possibile definire quella che viene chiamata
velocitá istantanea.
.
Se l'oggetto é in moto allora senz'altro é individuabile una variazione del
vettore r(t) e quindi é possibile definire quella che viene chiamata
velocitá istantanea.