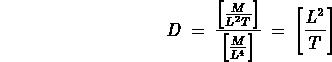macronote

NOTE

Con il simbolo si vuole indicare una differenza fra i valori assunti da una certa grandezza . Generalmente noi siamo interessati a differenze di valori fra punti molto vicini fra loro (nel tempo, nello spazio o in altre grandezze) in modo da poter fare considerazioni di validita` locale, (istante per istante, zona per zona...). Andando al limite possiamo considerare differenze di valori fra punti la cui distanza tende a 0. Non parleremo piu` di ma di d cioe` di differenziali. Inoltre la differenza fra i valori assunti da una funzione in due punti diviso la distanza fra i due punti, "portata al limite" sara` la derivata della funzione. Espresso in termini matematici:

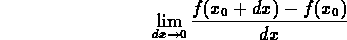
Questa e` la derivata della funzione f rispetto a x nel punto

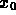L'equazione e` applicabile solo in sistemi dove la miscelazione dei componenti non e` accompagnata da cambiamenti di volume

La legge di Fick rientra in una classe molto ampia di relazioni fenomenologiche (relazioni derivate da osservazioni sperimentali) che legano un flusso (di massa, energia, cariche elettriche, ecc.) alla forza generalizzata che sostiene tale flusso (differenza di pressione, di concentrazione, di potenziale, ecc.)tramite un coefficiente di proporzionalita' che viene detto una permeabilita' generalizzata.

Altri esempi di simili relazioni sono la legge di D'Arcy che pone un flusso di liquido pari alla differenza di pressione idrostatica moltiplicata per la permeabilita' (inverso della resistenza idraulica), oppure la legge di Ohm, secondo cui la corrente elettrica e'proporzionale alla differenza di potenziale elettrico (tramite un coefficiente detto conducibilita').

La dipendenza dalla temperatura di D e` formalizzata dalla seguente relazione:

(*)

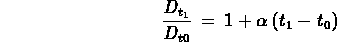dove a e` l'incremento frazionale di D dovuto ad un aumento di temperatura di un grado. La determinazione di a per varie sostanze e` stata fatta da Öholm.
Dal momento che il valore di D per una data sostanza dipende dalle condizioni sperimentali queste devono essere sempre specificate.

Considerazioni dimensionali per D
J e` un flusso di materia per superficie e` quindi una misura di massa per (su) superficie nel tempo:

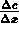e` una massa su volume (la concentrazione), su spazio

Dalla prima legge di Fick si ha che:

quindi dimensionalmente si trova:

Il principio di conservazione della massa e` valido nell'ambito della fisica classica e della chimica. La massa quindi e` un invariante per trasformazioni galileiane (le formule classiche per la composizione dei moti) e per trasformazioni chimiche. Quando si entra nell'ambito della Fisica relativistica e si studiano i fenomeni che avvengono ad alte velocita` (e quindi alte energie) le trasformazioni di Galileo perdono la loro validita` e devono essere soppiantate da un nuovo gruppo di relazioni che le comprendano come caso limite: le trasformazioni di Lorentz.In queste trasformazioni la massa non e` piu` un invariante.

Se una soluzione e` costituita da diverse specie chimiche, tutte molto diluite entro il solvente comune e non interagenti fra loro in nessun modo, la diffusione delle varie specie avviene in maniera del tutto indipendente. Nel caso della diffusione in una sola direzione, la concentrazione dei soluti, punto per punto, e` data dalla somma delle concentrazioni di ogni singolo soluto.

Ritorna all'analisi dal punto di vista macroscopico