Prima Legge di Fick
Che cosa e` D?
Seconda Legge di Fick
La relazione che descrive il fenomeno della diffusione da un punto di vista macroscopico venne determinata sperimentalmente da Fick nel 1855, osservando come, a parità di temperatura, di sostanza diffondente e di solvente, la massa di sale che diffonde attraverso una determinata interfaccia fosse direttamente proporzionale al gradiente di concentrazione attraverso la superficie, all'area della superficie e alla durata del fenomeno osservato; infine, come esso risultasse sempre diretto dalle regioni a concentrazione maggiore verso quelle a concentrazione minore.
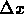
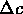misurata in tali punti
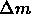che attraversa una area data A in
un tempo molto piccolo
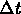
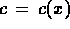cioè che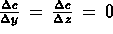 
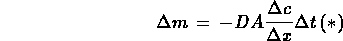
Dove D è una costante di proporzionalità.
Rispetto a dm è più interessante considerare J, il flusso di materia
attraverso la superficie, definito come portata di massa (quantità
di massa nel tempo) per unità di
superficie(1/A):
Allora la (*) si può scrivere nella forma più comune :
dove il segno meno sta ad indicare che il verso del flusso e' contrario al gradiente di concentrazione
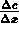
Così scritta, la legge di Fick non si limita semplicemente a formalizzare il fenomeno, ma separa le grandezze fisiche che in esso variano da quelle che rimangono costanti in ragione delle condizioni sperimentali che sono state imposte. D'altra parte, come è facile intuire, la temperatura, il tipo di soluto e quello di solvente sono parametri fisici molto importanti per il fenomeno in esame. Così ad esempio, è esperienza comune il fatto che lo zucchero si scioglie in minor tempo nel caffè bollente che in quello freddo; lo zucchero si scioglie in minor tempo nell'acqua che nel latte; l'alcool diffonde in acqua in minor tempo rispetto al vino. In realtà, la legge di Fick, scritta in questa forma, tiene conto anche della temperatura, del tipo di soluto e di solvente: infatti, al variare di una o più di queste grandezze fisiche varia la costante di proporzionalità D, cioè: D dipende dalla temperatura, dal tipo di soluto e di solvente. D è quindi un tipico esempio di parametro fenomenologico ed è chiamato coefficiente di diffusione.
La prima legge di Fick non e' sufficiente per risolvere completamente tutti i problemi di diffusione. Infatti basta notare che il flusso diffusionale puo' modificare il gradiente di concentrazione che spesso e' conseguentemente funzione del tempo.
Una seconda relazione interessante dalla quale si ricava
appunto la dipendenza della concentrazione dal tempo, si
ottiene ricordando che
deve essere sempre rispettato il
principio della conservazione della massa.
Questo si puo' esprimere con
una relazione che imponga che la variazione di
concentrazione della sostanza
in un volumetto infinitesimo aperto agli scambi di materia sia identica alla
differenza tra i flussi entrante e uscente nel medesimo elemento di volume, a
patto che non vi sia produzione della specie considerata all'interno del
volumetto stesso ad opera di qualche reazione chimica.
Supponendo nuovamente, per semplicità, che il fenomeno di diffusione avvenga unicamente nella direzione x,
si può osservare come la variazione della massa esterna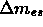 
ad un dato volume 
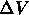debba essere equivalente alla variazione della massa interna 
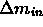allo stesso volume e cioè:
.
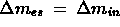In particolare, considerando la massa entrante nel volume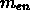 
e quella uscente 
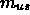, è possibile scrivere:
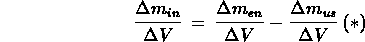
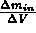è la concentrazione della sostanza considerata (
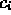) all'interno del volume e
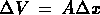. Quindi la (*) può essere riformulata nel modo seguente:
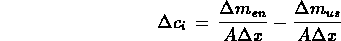
Considerando l'intervallo di tempo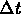 
in cui avviene il fenomeno:
Siccome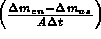 
è il flusso della sostanza attraverso il volume, è
possibile scrivere, a partire dalla 
, l'equazione di continuità:
Sostituendo a J la sua espressione data dalla prima legge di Fick si ottiene la seconda legge di Fick
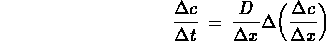
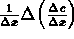può essere espresso in un modo più compatto
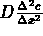e quindi la seconda legge di Fick si esprime come:
Poichè la teoria classica ( macroscopica) della diffusione introduce il coefficiente di diffusione come una grandezza sperimentalmente vincolata a valore costante, essa non dà alcuna indicazione per il suo calcolo, che deve quindi essere determinato sperimentalmente per ogni coppia di soluto e di solvente.
Classificazione dei fenomeni di diffusione
Note
Indice
Ritorna all'introduzione
Approssimazioni