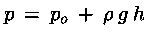LA LEGGE DI STEVINO

Possiamo ricavare la legge di Stevino in una maniera più rigorosa
considerando un piccolo elemento di fluido all'interno di un volume più
grande (finché non si procede all'integrazione, le equazioni che in
seguito verranno riportate saranno valide sia per i liquidi che per i
gas).

Questo elemento sia un disco sottile a distanza y sopra un
livello di riferimento ( dove sarà y = 0 ).
Ciascuna faccia del disco abbia area A e lo spessore sia dy.
In queste condizioni la massa di fluido contenuta nell'elemento di
volume sarà
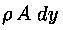 ed il suo peso
ed il suo peso
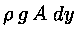 ; le
forze che agiscono sul volume in questione sono il suo peso e le forze
di pressione esercitate dal fluido circostante. Di queste ultime
consideriamo solo quelle del fluido a contatto con le due basi del
cilindro perché le forze dovute alla pressione del fluido sono in
ogni punto perpendicolari alla superficie dell'elemento stesso, per cui
per simmetria quelle agenti sulla superficie laterale si bilanciano tra
loro.
; le
forze che agiscono sul volume in questione sono il suo peso e le forze
di pressione esercitate dal fluido circostante. Di queste ultime
consideriamo solo quelle del fluido a contatto con le due basi del
cilindro perché le forze dovute alla pressione del fluido sono in
ogni punto perpendicolari alla superficie dell'elemento stesso, per cui
per simmetria quelle agenti sulla superficie laterale si bilanciano tra
loro.
Poiché l'elemento non ha accelerazione verticale, la forza risultante
(dovuta al fluido sovrastante e sottostante il volume e al peso
di quest'ultimo) agente sulla faccia inferiore del cilindro dovrà
essere nulla in tale direzione e quindi se p è la pressione
agente sulla faccia inferiore del disco, (p + dp) quella
agente sulla faccia superiore, le forze applicate alle due facce saranno
rispettivamente pA e (p + dp)A,
che sommate alla forza peso del fluido contenuto nel dischetto daranno
per la base inferiore un bilancio pari a :

Da cui ricaviamo
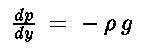
Questa equazione (che vale sia per i liquidi che per i gas)
ci dice come varia la pressione per un fluido in
equilibro statico in funzione della distanza a partire da un livello di
riferimento stabilito.
Se dalla quota di riferimento p1 è la pressione
a quota y1 e p2 quella relativa alla
quota y2, integrando l'equazione sopra si ha:
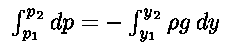
ovvero
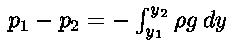
Ora nel caso di un liquido omogeneo possiamo considerare
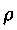 e g costanti, rispettivamente per il fatto che i liquidi sono
praticamente incomprimibili e quindi la loro densità non varia
e perché le differenze di quota che andiamo a considerare ci permettono
di trascurare le variazioni di g con l'altezza. In queste condizioni
l'integrazione dà l'equazione (valida solo per i liquidi):
e g costanti, rispettivamente per il fatto che i liquidi sono
praticamente incomprimibili e quindi la loro densità non varia
e perché le differenze di quota che andiamo a considerare ci permettono
di trascurare le variazioni di g con l'altezza. In queste condizioni
l'integrazione dà l'equazione (valida solo per i liquidi):
![p(2)-p(1)=- ro*g*[y(2)-y(1)]](/mflu/imgs/formule/stevdif.gif)
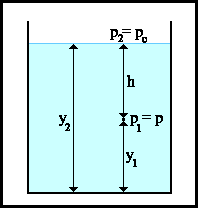
Nel caso della figura, prendendo come livello di riferimento la superficie
libera del fluido dove si considera una pressione po
e misurando le quote dal fondo del recipiente ( per cui h è
il dislivello ( y2 - y1 )
) , la pressione p per un punto a quota
y1 si scrive più semplicemente :
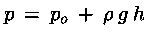
 Variazioni di pressione nei fluidi <
Variazioni di presione nei liquidi < La legge di Stevino
Variazioni di pressione nei fluidi <
Variazioni di presione nei liquidi < La legge di Stevino
 Indice
Indice
Copyright © I.S.H.T.A.R. - March, 1999

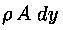 ed il suo peso
ed il suo peso
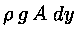 ; le
forze che agiscono sul volume in questione sono il suo peso e le forze
di pressione esercitate dal fluido circostante. Di queste ultime
consideriamo solo quelle del fluido a contatto con le due basi del
cilindro perché le forze dovute alla pressione del fluido sono in
ogni punto perpendicolari alla superficie dell'elemento stesso, per cui
per simmetria quelle agenti sulla superficie laterale si bilanciano tra
loro.
; le
forze che agiscono sul volume in questione sono il suo peso e le forze
di pressione esercitate dal fluido circostante. Di queste ultime
consideriamo solo quelle del fluido a contatto con le due basi del
cilindro perché le forze dovute alla pressione del fluido sono in
ogni punto perpendicolari alla superficie dell'elemento stesso, per cui
per simmetria quelle agenti sulla superficie laterale si bilanciano tra
loro.
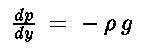
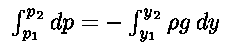
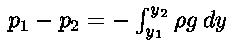
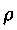 e g costanti, rispettivamente per il fatto che i liquidi sono
praticamente incomprimibili e quindi la loro densità non varia
e perché le differenze di quota che andiamo a considerare ci permettono
di trascurare le variazioni di g con l'altezza. In queste condizioni
l'integrazione dà l'equazione (valida solo per i liquidi):
e g costanti, rispettivamente per il fatto che i liquidi sono
praticamente incomprimibili e quindi la loro densità non varia
e perché le differenze di quota che andiamo a considerare ci permettono
di trascurare le variazioni di g con l'altezza. In queste condizioni
l'integrazione dà l'equazione (valida solo per i liquidi):
![p(2)-p(1)=- ro*g*[y(2)-y(1)]](/mflu/imgs/formule/stevdif.gif)