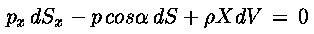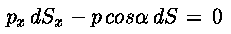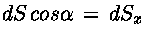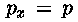PRESSIONE E ORIENTAZIONE DELLE
SUPERFICI

I fluidi sono stati definiti come quei mezzi che in equilibrio possono
sopportare sforzi normali alle rispettive superfici. Una conseguenza
immediata di questo è che in equilibrio la pressione su tutti
gli elementi di superficie che passano per uno stesso punto è la
stessa qualunque sia la loro orientazione.
Consideriamo (all'interno di una massa fluida in quiete) una terna di assi
cartesiani con origine in O: un piano generico ABC molto
prossimo ad O isola una porzione di fluido di volume infinitesimo
a forma di tetraedro. Il tetraedro è soggetto al peso e alle forze di
pressione agenti sulle quattro facce.
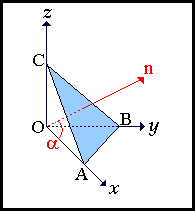
Indichiamo con px ,py ,
pz le pressioni sulle tre facce normali rispettivamente
agli assi x, y, z e di area dSx ,
dSy ,dSz; con p la pressione
sulla faccia ABC di area dS. Sappiamo che le pressioni sono
normali alle rispettive facce. La componente di p secondo x
è
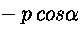 se
se 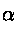 è l'angolo tra x e la normale ad ABC diretta verso
l'esterno del tetraedro. Le componeti della forza di massa applicata
al tetraedro rispetto agli assi saranno
è l'angolo tra x e la normale ad ABC diretta verso
l'esterno del tetraedro. Le componeti della forza di massa applicata
al tetraedro rispetto agli assi saranno
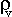 ,
,
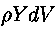 ,
,
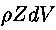 .
Per l'equilibrio si dovrà avere:
.
Per l'equilibrio si dovrà avere:
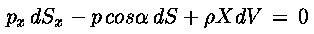
Se il tetraedro è infinitesimo e si assume la lunghezza dei lati come
infinitesimo del primo ordine, ne segue che l'area delle facce è
infinitesima del secondo ordine ed il volume del terzo ordine. In queste
condizioni è lecito trascurare quello del terzo ordine come
infinitesimo di ordine superiore: le forze di volume tendono a zero, quando
le domensioni tendono a zero, poiché tende a zero il rapporto tra
volume e superficie. Ne segue che:
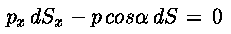
e poiché:
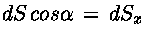
si ha:
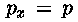
Con lo stesso procedimento si otterrebbe py = pz =
p, e quindi
dal fatto che la pressione non dipende dall'orientazione dell'elemento di
superficie al quale è applicata, si può parlare di pressione
nel punto O, senza specificare una superficie sulla quale esso agisca.
 La pressione nei fluidi
La pressione nei fluidi
 Indice
Indice
Copyright © I.S.H.T.A.R. - March, 1999

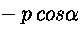 se
se 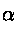 è l'angolo tra x e la normale ad ABC diretta verso
l'esterno del tetraedro. Le componeti della forza di massa applicata
al tetraedro rispetto agli assi saranno
è l'angolo tra x e la normale ad ABC diretta verso
l'esterno del tetraedro. Le componeti della forza di massa applicata
al tetraedro rispetto agli assi saranno
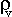 ,
,
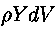 ,
,
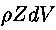 .
Per l'equilibrio si dovrà avere:
.
Per l'equilibrio si dovrà avere: