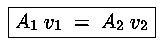L'EQUAZIONE DI CONTINUITÀ

Abbiamo detto che considereremo lo spazio occupato dal fluido come
un campo vettoriale, ma con ciò non abbandoneremo neanche la
visione lagrangiana del problema, prendendo in esame il moto delle
particelle costituenti il fluido, che poi è quello che più
direttamente ci interessa.
Useremo il termine particella in senso newtoniano, cioè
con riferimento ad una massa puntiforme
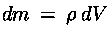 e ad un elemento di volume
e ad un elemento di volume
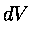 così piccolo da poter considerare le forze che su di esso agiscono
come applicate ad un unico punto, ma anche sufficientemente grande da
contenere un elevato numero di molecole cosicché la media delle
velocità disordinate di queste ultime sia nulla.
così piccolo da poter considerare le forze che su di esso agiscono
come applicate ad un unico punto, ma anche sufficientemente grande da
contenere un elevato numero di molecole cosicché la media delle
velocità disordinate di queste ultime sia nulla.
In quest'ottica considerando il flusso stazionario di un fluido
all'interno di un tubo di flusso di sezione variabile, ma ponendoci
nella condizione più generale per cui detto fluido sia comprimibile,
vediamo cosa accade all'interno del tubo tenendo presente la validità
delle leggi di conservazione di massa ed energia.
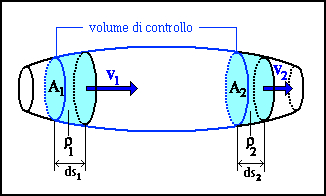
Il volume di controllo che prendiamo in considerazione sarà
contenuto nel tubo tra due sezioni A1 ed A2, dove le
densità del fluido stesso sranno rispettivamente
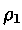 e
e
 .
.
Se nel tempo dt entra una certa massa di fluido attraverso
A1, occupando il volume A1ds1, nello
stesso intervallo infinitesimo di tempo una massa della stessa entità
ma di volume A2ds2 dovrà uscire dal tubo,
proprio perché per la conservazione della massa all'interno del tubo
non ci potrà essere creazione o distruzione di materia. Ne seguirà
che :
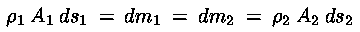
Dividendo entrambi i membri per dt otteniamo così
l'equazione di continuità per un generico fluido in flusso stazionario
(per ottenere questa equazione non è necessario supporre il fluido
incomprimibile):
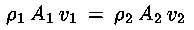
L'equazione appena scritta stabilisce inoltre, per l'arbitrarietà
delle sezioni A1 e A2, che la massa di fluido
che attraversa una sezione del tubo di flusso in un secondo nelle
condizioni di flusso stazionario è costante.
Nel caso di un flusso incomprimibile, cioè per
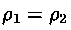 la relazione sopra si riduce a :
la relazione sopra si riduce a :
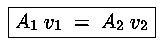
Per lo stesso motivo di cui sopra il prodotto Av
sarà costante lungo il tubo, il che equivale a dire che la
velocità nel tubo di flusso è inversamente proporzionale alla
sua sezione. Nella rappresentazione mediante linee di flusso in questi
casi si hanno perciò zone di bassa velocità dove queste sono
più rade, zone di alta velocità dove sono più fitte.
 Fluidi ideali < Equazione di continuità
(Pagina principale)
Fluidi ideali < Equazione di continuità
(Pagina principale)
 Indice
Indice
Copyright © I.S.H.T.A.R. - March, 1999
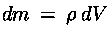 e ad un elemento di volume
e ad un elemento di volume
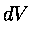 così piccolo da poter considerare le forze che su di esso agiscono
come applicate ad un unico punto, ma anche sufficientemente grande da
contenere un elevato numero di molecole cosicché la media delle
velocità disordinate di queste ultime sia nulla.
così piccolo da poter considerare le forze che su di esso agiscono
come applicate ad un unico punto, ma anche sufficientemente grande da
contenere un elevato numero di molecole cosicché la media delle
velocità disordinate di queste ultime sia nulla.
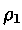 e
e
 .
.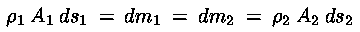
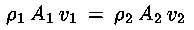
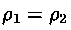 la relazione sopra si riduce a :
la relazione sopra si riduce a :