Supponiamo di avere un condotto di sezione variabile. Per ipotesi il
fluido sia incomprimibile (viscoso o meno):
ad un certo volume
di fluido entrante nel tubo corrisponderà un ugual volume di fluido
uscente .
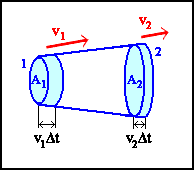
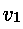 e la sezione del condotto è A1, nell'intervallo di tempo
e la sezione del condotto è A1, nell'intervallo di tempo
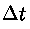 sarà passato un volume di fluido
sarà passato un volume di fluido
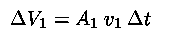
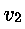 corrispondente ad una sezione A2 del tubo. Nello stesso
intervallo
corrispondente ad una sezione A2 del tubo. Nello stesso
intervallo
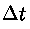 di tempo uscirà quindi dal punto 2 un volume di fluido
di tempo uscirà quindi dal punto 2 un volume di fluido
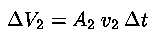
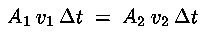
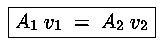
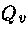 e
dall'equazione di continuità si deduce che in una corrente
stazionaria di un fluido incompressibile la portata in volume ha lo
stesso valore in ogni punto del fluido :
e
dall'equazione di continuità si deduce che in una corrente
stazionaria di un fluido incompressibile la portata in volume ha lo
stesso valore in ogni punto del fluido :
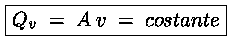
 Note
Note
 Esercizi
Esercizi
 Esempi
Esempi
 Approfondimento matematico: l'equazione di continuità
Approfondimento matematico: l'equazione di continuità