LA EQUAZIONE DI BERNOULLI

Consideriamo ora un fluido ideale che scorra in un tubo di sezione e quota
variabile :
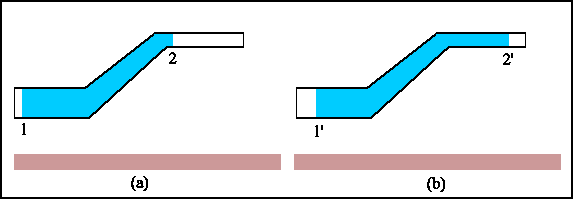
Lo spostamento del fluido nel condotto porterà la massa che si trova
tra i punti 1 e 2 a trovarsi dopo un intervallo di tempo
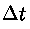 tra i punti 1' e 2'. La variazione tra le figure (a) e (b)
riguarda le porzioni di massa fluida ombreggiate nella figura sotto
(in
figura sono indicati i moduli dei vettori disegnati: in tutta questa
sezione tratteremo direttamente con i moduli delle grandezze vettoriali in
questione):
tra i punti 1' e 2'. La variazione tra le figure (a) e (b)
riguarda le porzioni di massa fluida ombreggiate nella figura sotto
(in
figura sono indicati i moduli dei vettori disegnati: in tutta questa
sezione tratteremo direttamente con i moduli delle grandezze vettoriali in
questione):
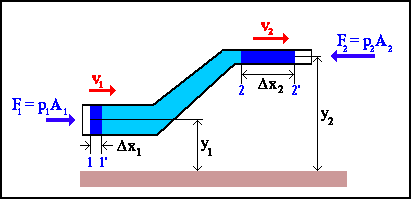
Il volume entrante sarà uguale a quello uscente
(per l'incomprimibilità):
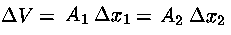
e la massa di questo fluido sarà:
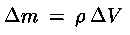
Per effetto del movimento del fluido la massa
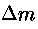 nel tempo
nel tempo
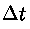 è stata spostata dalla quota y1
alla quota y2 e la sua velocità è variata
da v1 a v2.
è stata spostata dalla quota y1
alla quota y2 e la sua velocità è variata
da v1 a v2.
Per trovare una legge che regola il moto in questo tipo di condotto è
necessario applicare il teorema dell'energia cinetica al fluido contenuto
inizialmente tra i punti 1 e 1' ovvero alla
massa di fluido
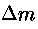 .
.
La variazione di energia cinetica di questa massa è
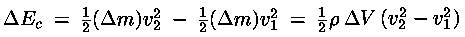
La variazione di energia potenziale è:
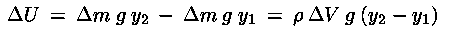
Il fluido a sinistra dell'imboccatura del tubo che precede la massa
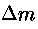 eserciterà su essa una forza di modulo
eserciterà su essa una forza di modulo
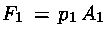 , dove p1 è la pressione nel punto 1.
Questa forza compirà un lavoro :
, dove p1 è la pressione nel punto 1.
Questa forza compirà un lavoro :
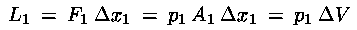
Con un ragionamento analogo, alla fine del tubo, a destra della massa
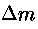 considerata, il fluido che segue compirà su di essa un lavoro negativo:
considerata, il fluido che segue compirà su di essa un lavoro negativo:
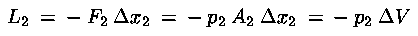
dove p2 è la pressione nel punto 2 esercitata in
verso contrario al moto del fluido.
Il lavoro totale compiuto da queste forze è :
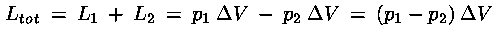
e quindi dal teorema dell'energia cinetica
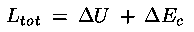
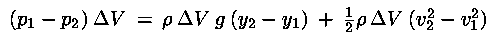
dividendo per
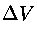 e raccogliendo al primo membro le grandezze relative al
punto 1 ed al secondo quelle relative al punto 2 :
e raccogliendo al primo membro le grandezze relative al
punto 1 ed al secondo quelle relative al punto 2 :
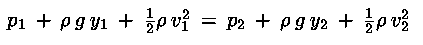
Poiché i due punti sono stati presi a caso nel condotto è possibile
ripetere questo ragionamento per qualsiasi coppia di punti e quindi
concludere che
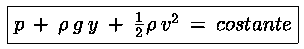
detta equazione di Bernoulli.
L'equazione di Bernoulli è rigorosamente applicabile solo a moti
stazionari poiché le grandezze che intervengono devono venir valutate
lungo una stessa linea di flusso : la costante che compare nell'equazione
non è in generale la stessa per tutte le linee di flusso.
Se il flusso è
irrotazionale si può dimostrare che la costante è la
stessa per tutte le linee di flusso.
È da notare inoltre che, come per le particelle materiali, le leggi
della statica sono un caso particolare di quelle della dinamica :
considerando infatti il caso in cui
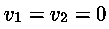 la penultima equazione si può anche scrivere come
la penultima equazione si può anche scrivere come
![p(2)-p(1)=-ro*g*[y(2)-y(1)]](/mflu/imgs/formule/diffp1.gif)
che è una delle forme in cui possiamo scrivere la legge di
Stevino.
La pressione
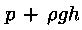 che sarebbe presente anche se non vi fosse moto si chiama pressione
statica; il temine
che sarebbe presente anche se non vi fosse moto si chiama pressione
statica; il temine
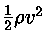 si chiama pressione dinamica.
si chiama pressione dinamica.
 Quesito
Quesito
 Esercizi
Esercizi
 Applicazioni
Applicazioni
 Esempi
Esempi
 Storia
Storia
 Approfondimento matematico: l'equazione di
Bernoulli
Approfondimento matematico: l'equazione di
Bernoulli
 Fluidi ideali > Effetto Venturi
Fluidi ideali > Effetto Venturi
 Fluidi ideali < Equazione di continuità
Fluidi ideali < Equazione di continuità
 Indice
Indice
Copyright © I.S.H.T.A.R. - March, 1999

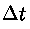 tra i punti 1' e 2'. La variazione tra le figure (a) e (b)
riguarda le porzioni di massa fluida ombreggiate nella figura sotto
(in
figura sono indicati i moduli dei vettori disegnati: in tutta questa
sezione tratteremo direttamente con i moduli delle grandezze vettoriali in
questione):
tra i punti 1' e 2'. La variazione tra le figure (a) e (b)
riguarda le porzioni di massa fluida ombreggiate nella figura sotto
(in
figura sono indicati i moduli dei vettori disegnati: in tutta questa
sezione tratteremo direttamente con i moduli delle grandezze vettoriali in
questione):

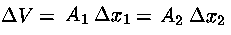
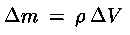
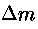 nel tempo
nel tempo
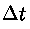 è stata spostata dalla quota y1
alla quota y2 e la sua velocità è variata
da v1 a v2.
è stata spostata dalla quota y1
alla quota y2 e la sua velocità è variata
da v1 a v2.
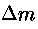 .
.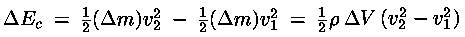
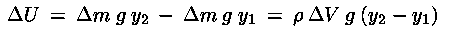
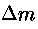 eserciterà su essa una forza di modulo
eserciterà su essa una forza di modulo
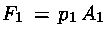 , dove p1 è la pressione nel punto 1.
Questa forza compirà un lavoro :
, dove p1 è la pressione nel punto 1.
Questa forza compirà un lavoro :
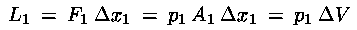
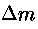 considerata, il fluido che segue compirà su di essa un lavoro negativo:
considerata, il fluido che segue compirà su di essa un lavoro negativo:
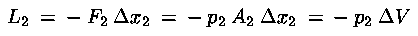
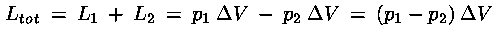
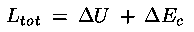
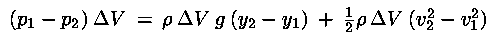
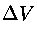 e raccogliendo al primo membro le grandezze relative al
punto 1 ed al secondo quelle relative al punto 2 :
e raccogliendo al primo membro le grandezze relative al
punto 1 ed al secondo quelle relative al punto 2 :
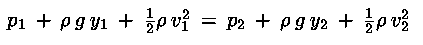
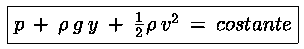
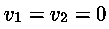 la penultima equazione si può anche scrivere come
la penultima equazione si può anche scrivere come
![p(2)-p(1)=-ro*g*[y(2)-y(1)]](/mflu/imgs/formule/diffp1.gif)
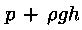 che sarebbe presente anche se non vi fosse moto si chiama pressione
statica; il temine
che sarebbe presente anche se non vi fosse moto si chiama pressione
statica; il temine
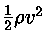 si chiama pressione dinamica.
si chiama pressione dinamica.
 Quesito
Quesito
 Esercizi
Esercizi
 Applicazioni
Applicazioni
 Esempi
Esempi
 Storia
Storia
 Approfondimento matematico: l'equazione di
Bernoulli
Approfondimento matematico: l'equazione di
Bernoulli