L'EQUAZIONE DI BERNOULLI

====================================


Attraverso il principio di conservazione dell'energia è possibile ricavare una relazione indipendente per il flusso stazionario di un fluido incomprimibile (e quindi in questo caso 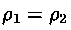ro(1)=ro(2) ) e non viscoso.
Ancora una volta prendiamo in considerazione un tubo a sezione variabile che conduca il fluido a quote diverse : come nel caso dell'equazione di continuità per un volume dV di fluido che attraversi la sezione A1, ce ne sarà uno uguale che attraverserà A2.
Il fluido a sinistra di A1 agisce quindi come un pistone costringendo il volume dV = A1· ds1 ad attraversare A1 : detta p1 la pressione in A1 il lavoro infinitesimo compiuto sul fluido sarà perciò :

dW(1)=F(1)*ds(1)=p(1)*A(1)*ds(1)=p(1)*dV

Allo stesso tempo il fluido compreso tra A1 ed A2 costringe una parte di fluido ad attraversare A2 e compie il lavoro dW2 = p 2 · dV. Il lavoro compiuto complessivamente sul fluido del volume di controllo è quindi :

dW=[p(1)-p(2)]*dV

Trascurando l'attrito tale lavoro si trasformerà in aumento di energia cinetica e potenziale del fluido. L'aumento di energia cinetica in dV conseguente al passaggio da A1 ad A2 sarà :

dK = (1/2)*ro*[v(2)*v(2) -v(1)*v(1)]*dV

mentre quello di energia potenziale :

dU(g) = ro*g*[y(2) - y(1)]*dV

Per il principio di conservazione dell'energia sarà quindi:

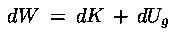
dW=dK+dU

da cui

[p(1) - p(2)]*dV = (1/2)*ro*[v(2)*v(2) -v(1)*v(1)]*dV + ro*g*[y(2) - y(1)]*dV

e quindi

alt=

che, poiché i due punti sono stati presi a caso, si può generalizzare nell'equazione di Bernoulli :

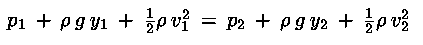
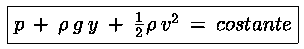
p + ro*g*y + (1/2)*ro*v*v = costante

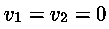Il caso statico, nel quale v(1)=v(2)=0 ritroviamo la Legge di Stevino:

p(2)-p(1)=- ro*g*[y(2)-y(1)]

<--  Fluidi ideali < Equazione di Bernoulli (Pagina principale)
indice  Indice

Copyright © I.S.H.T.A.R. - March, 1999