GENERALITÀ

Per studiare il moto di un fluido sotto l'azione di forze possiamo, generalizzando i concetti della meccanica del punto materiale sviluppati da Lagrange, suddividere il fluido in elementi di volume infinitesimi ( detti particelle di fluido ) e seguirne il moto.
Questo modo di procedere ci impone però di dare le coordinate x, y, z di ciascuna particella e di precisarne il comportamento in funzione del tempo t: è questo un compito improbo in quanto le coordinate x, y, z al tempo t saranno funzione del tempo stesso e delle coordinate x_o , y_o , z_o della particella relative al tempo t_o.
È possibile descrivere il moto del fluido in modo più semplice determinando densità e velocità del fluido in ciascun punto dello spazio ed in ogni istante.
Questo sarà il modo di procedere da questo momento in poi : vedremo cosa accade in un dato punto dello spazio e in un dato istante, anche se non potremo evitare completamente di seguire le particelle fluide nel loro moto, almeno per piccoli intervalli di tempo dt, visto che è alle particelle e non ai punti dello spazio che si devono applicare le leggi della meccanica.

Un primo esempio di questo nostro modo di procedere lo abbiamo definendo lo spazio occupato dal fluido in moto come un campo vettoriale. Introducendo nel fluido in moto delle particelle eterogenee che rimangano in sospensione si rende visibile il moto del fluido: nei liquidi è in uso introdurre polvere di alluminio, nei gas si usano dei fumi o delle nebbie. Queste eterogeneità non influiscono sensibilmente sul moto ma servono ad individuare i singoli elementi di volume del fluido e possono essere fotografate : un'istantanea che duri un tempo 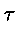dà per ogni particella un tratto di lunghezza proporzionale a 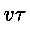, cioè allo spazio percorso nel tempo 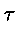, e quindi proporzionale alla velocità dell'elemento e diretto come questa. È possibile avere in questo modo una visione di insieme del moto degli elementi costituenti il fluido nelle varie parti della corrente e vedere appunto quest'ultima come campo vettoriale : il vettore velocità ad un dato istante è funzione dei punti dello spazio ed è proprio così che si passa dal moto della singola particella allo studio del moto del fluido nel suo insieme attraverso i valori che assumono nel tempo le grandezze che lo caratterizzano (velocità, densità e pressione).

Copyright © I.S.H.T.A.R. - March, 1999