LA RESISTENZA AL MOTO DI UN CORPO IN UN FLUIDO

I concetti di moto laminare e vorticoso possono essere estesi al caso di
un corpo che sia in moto rispetto al fluido in cui è immerso.
Mettendosi in un sistema di riferimento solidale al corpo, il numero
di Reynolds per il moto del corpo con velocità v relativa
al fluido avrà forma analoga all'espressione precedente:

dove questa volta d indica il diametro medio del corpo.
Il problema della forza esercitata da un fluido viscoso su un corpo
in esso immerso è complesso. George Stokes, nel 1845, prese in
considerazione il problema solo per un caso particolare, quello di
un oggetto di forma sferica, completamente immerso in un fluido in
moto laminare, di densità costante ed incomprimibile.
Per questa
situazione egli ricavò che il modulo della forza
di attrito che agisce sul corpo si esprime come:
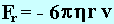
detta legge di Stokes. In questa formula
Fr è il modulo della forza ritardante,
 è
il coefficiente di viscosità del fluido, r è il raggio
della
sfera e v il modulo della velocità della sfera rispetto il
fluido.
è
il coefficiente di viscosità del fluido, r è il raggio
della
sfera e v il modulo della velocità della sfera rispetto il
fluido.
La formula sia stata ricavata per un oggetto di forma sferica
essa può essere applicata in molte situazioni (cambierà il valore
delle costanti di proporzionalità): dai fenomeni
metereologici alle particelle in sospensione in un fluido.
Verifichiamo la plausibilità di questa formula attraverso l'analisi
dimensionale: è ragionevole supporre che la forza ritardante agente
sul corpo immeso nella corrente fluida sia proporzionale ad una qualche
potenza della viscosità, del raggio della sfera e della velocità,
e che sia tale da opporsi alla direzione del moto. Per il modulo di
questa forza possiamo allora scrivere:

Riducendo le quantità elencate alle dimensioni fondamentali si ha:
M L T-2 = (M L-1 T-1)a
Lb (L T-1)c
Imponendo la coerenza dimensionale dei fattori corrispondenti nei due
mambri si ha:
| per M | 1 = a
|
| per L | 1 = - a + b + c
|
| per T | - 2 = - a - c
|
sistema che risolto dà a = 1, b = 1 e c = 1,
proprio come nell'equazione sopra, posto il coefficiente
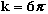 .
.
Se il moto invece è turbolento le forze inerziali
dominano su quelle viscose e la forza di resistenza è:

Infatti se consideriamo un cilindro di fluido con immersa in esso una
sfera di sezione A e immaginiamo che il fluido che entra a
contatto con la sfera perda mediamente metà della propria quantità
di moto nella direzione di avanzamento, poiché la massa che
nell'unità di tempo subisce una perdita di velocità pari a
1/2 v è
(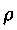 vA)
,
la forza di reazione inerziale che agisce sulla sfera è
proporzionale a
(1/2
vA)
,
la forza di reazione inerziale che agisce sulla sfera è
proporzionale a
(1/2
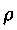 v²
A). La costante c che compare nella formula sopra è
chiamata coefficiente di resistenza.
v²
A). La costante c che compare nella formula sopra è
chiamata coefficiente di resistenza.
 Fluidi viscosi < Il moto vorticoso
Fluidi viscosi < Il moto vorticoso
 Indice
Indice
Copyright © I.S.H.T.A.R. - March, 1999

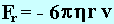
 è
il coefficiente di viscosità del fluido, r è il raggio
della
sfera e v il modulo della velocità della sfera rispetto il
fluido.
è
il coefficiente di viscosità del fluido, r è il raggio
della
sfera e v il modulo della velocità della sfera rispetto il
fluido.
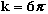 .
.
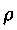 vA)
,
la forza di reazione inerziale che agisce sulla sfera è
proporzionale a
(1/2
vA)
,
la forza di reazione inerziale che agisce sulla sfera è
proporzionale a
(1/2
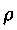 v²
A). La costante c che compare nella formula sopra è
chiamata coefficiente di resistenza.
v²
A). La costante c che compare nella formula sopra è
chiamata coefficiente di resistenza.