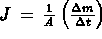 e l'illustrazione del principio
di conservazione della massa si
giunge alla formulazione matematica delle leggi nella forma seguente:
e l'illustrazione del principio
di conservazione della massa si
giunge alla formulazione matematica delle leggi nella forma seguente:
In questa sezione sono ricavate le due leggi stabilite da Fick nel 1855 in base alle osservazioni sperimentali che sono descritte, nel caso in cui il flusso si possa considerare lungo una sola direzione.
Dopo l'introduzione dei concetti di ``flusso''
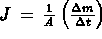 e l'illustrazione del principio
di conservazione della massa si
giunge alla formulazione matematica delle leggi nella forma seguente:
e l'illustrazione del principio
di conservazione della massa si
giunge alla formulazione matematica delle leggi nella forma seguente:
I legge di Fick:
II legge di Fick:
dove
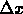 e
e 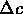 sono rispettivamente la distanza e la differenza di
concentrazione fra
due punti in una soluzione e
D è il coefficiente di diffusione.
sono rispettivamente la distanza e la differenza di
concentrazione fra
due punti in una soluzione e
D è il coefficiente di diffusione.
Si precisa che ogni formula rappresenta una relazione fra
grandezze fisiche,
ricavata proprio in seguito alla osservazione
di come esse variano.
Sono fatte notare le dipendenze del coefficiente di diffusione  (tipico esempio di parametro fenomenologico) dalle grandezze fisiche coinvolte
nel fenomeno che non appaiono esplicitamenete nelle formule (tipo di
soluto e di solvente, concentrazione, temperatura [26]) e che rimangono
costanti in ragione delle condizioni sperimentali imposte.
(cfr. appendice A.3)
(tipico esempio di parametro fenomenologico) dalle grandezze fisiche coinvolte
nel fenomeno che non appaiono esplicitamenete nelle formule (tipo di
soluto e di solvente, concentrazione, temperatura [26]) e che rimangono
costanti in ragione delle condizioni sperimentali imposte.
(cfr. appendice A.3)
In tutto il discorso si vuole trasmettere che l'uso del linguaggio matematico nella Fisica si è instaurato perchè esso è il più adatto per descrivere sinteticamente e precisamente come si comporta la Natura.
Nelle pagine principali viene utilizzata una
matematica di base in
modo da non mettere a disagio studenti novizi.
Si ritiene che i passaggi possano
essere seguiti anche da studenti agli ultimi anni delle scuole superiori
dal momento che non sono richieste conoscenze di analisi matematica.
Invece di considerare differenziali si parla di ``quantitá
molto piccole'' ( ) e piuttosto che esporre i passaggi matematici si
preferisce dire che il ``buon senso'', sempre alla luce delle osservazioni
sperimentali, suggerisce che le cose debbano andare
in un certo modo; ecco dunque la formulazione di una ipotesi e,
dietro verifica, la scoperta di una nuova legge.
Comunque le formule presentate sono sufficienti per risolvere
sempici esercizi e le dimostrazioni per via matematica sono a disposizione
in pagine di complementi in cui vengono anche offerti spunti di
riflessione, note sulla parte più strettamente sperimentale, cenni di teoria
degli errori, agganci con altre discipline o con altri rami della Fisica ecc..
) e piuttosto che esporre i passaggi matematici si
preferisce dire che il ``buon senso'', sempre alla luce delle osservazioni
sperimentali, suggerisce che le cose debbano andare
in un certo modo; ecco dunque la formulazione di una ipotesi e,
dietro verifica, la scoperta di una nuova legge.
Comunque le formule presentate sono sufficienti per risolvere
sempici esercizi e le dimostrazioni per via matematica sono a disposizione
in pagine di complementi in cui vengono anche offerti spunti di
riflessione, note sulla parte più strettamente sperimentale, cenni di teoria
degli errori, agganci con altre discipline o con altri rami della Fisica ecc..
Nella pagina di note si osserva che la prima legge di Fick
rientra in una
classe molto ampia di relazioni fenomenologiche [25]
(derivate da osservazioni sperimentali) che legano un flusso alla forza
generalizzata che sostiene tale
flusso tramite un coefficiente di proporzionalitá (permeabilitá
generalizzata).
Esempi di relazioni di questo tipo sono la legge di
D'Arcy che pone un flusso di liquido pari alla differenza di pressione
idrostatica moltiplicata per la permeabilità e la legge di Ohm secondo la
quale la corrente elettrica è proporzionale alla differenza di potenziale
elettrico per la
conducibilità![]() .
.