

Esiste un modo elegante per ricavare quella che noi abbiamo
dato come definizione di media pesata.
Supponiamo come nel caso precedente di avere due misure della
stessa grandezza (X) così definite:
prima misura: 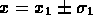
seconda misura: 
Se assumiamo che entrambe le misure siano governate dalla
distribuzione di Gauss (normale), allora la probabilità
che il primo osservatore, all'atto della misura ottenga proprio
il valore 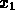 è:
è:
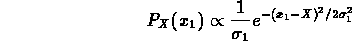
mentre per il secondo osservatore, la probabilità di ottenere
il valore 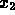 è:
è:
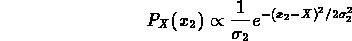
Potendo considerare le due misure come eventi indipendenti, si
ha che la probabilità che contemporaneamente i due osservatoti
trovino i due valori 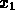 e
e 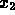 è pari al prodotto
delle singole probabilità, percui:
è pari al prodotto
delle singole probabilità, percui:
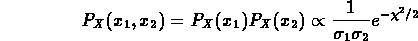
Nell'ultima espressione abbiamo utilizzato il simbolo  per abbreviare la
seguente espressione:
per abbreviare la
seguente espressione:
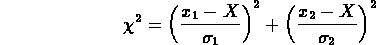
Questa importante grandezza, la somma dei quadrati delle deviazioni da X delle due misure, ciascuna divisa per la corrispondente incertezza, è talvolta chiamata "somma dei quadrati"
Ora, la nostra miglior stima per il valore vero della
grandezza incognita X è rappresentato da quel valore
percui le effettive misurazioni 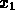 e
e 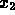 hanno probabilità massima, ossia in
corrispondenza di un minimo dell'esponente
hanno probabilità massima, ossia in
corrispondenza di un minimo dell'esponente  : poichè massimizzare la
probabilità equivale a minimizzare la cosiddetta somma dei
quadrati, questo metodo è anche detto metodo dei minimi
quadrati.
: poichè massimizzare la
probabilità equivale a minimizzare la cosiddetta somma dei
quadrati, questo metodo è anche detto metodo dei minimi
quadrati.
Così, per trovare la miglior stima, differenziamo rispetto ad X
e poniamo la derivata uguale a zero:
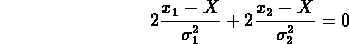
eseguendo i calcoli si ricava:

Questa espressione può essere resa più semplice introducendo le definizioni di pesi:

Se sostituiamo quest'ultima nella precedente otteniamo:

Il risultato così ottenuto può venire facilmente generalizzato al caso di N misure con le relative incertezze, ottenendo così la già introdotta definizione di media pesata.
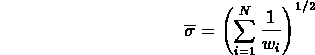
percui in definitiva possiamo esprimere il risultato nella forma:
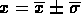
 La media pesata
La media pesata