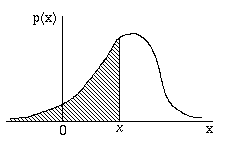Vediamo ora in dettaglio le due funzioni fondamentali che abbiamo introdotto: la funzione di distribuzione cumulativa e la funzione densità di probabilità.
Consideriamo una variabile aleatoria continua X con
densità di probabilità p(x) e il dominio elementare dx
adiacente al punto x. La probabilità che tale variabile
appartenga a questo intervallo è pari a p(x)dx: la
quantità p(x)dx si chiama elemento di probabilità
(zona tratteggiata nel Grafico 1).
Se ora vogliamo esprimere la probabilità che la variabile
aleatoria appartenga all'intervallo (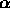 ,
,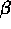 ) in funzione della densità di
probabilità, otteniamo
) in funzione della densità di
probabilità, otteniamo
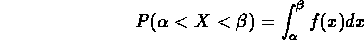
che rappresenta la somma di tutti gli elementi di
probabilità sull'intervallo (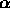 ,
,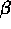 ).
).
Dal punto di vista geometrico la probabilità che la variabile
aleatoria X appartenga all'intrevallo (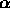 ,
,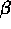 ) è uguale all'area compresa tra la
curva definita della densità di probabilità (detta curva di
densità) e l'asse delle ascisse, limitata dagli estremi
dell'intervallo (zona tratteggiata nel Grafico 2).
) è uguale all'area compresa tra la
curva definita della densità di probabilità (detta curva di
densità) e l'asse delle ascisse, limitata dagli estremi
dell'intervallo (zona tratteggiata nel Grafico 2).
Grafico 1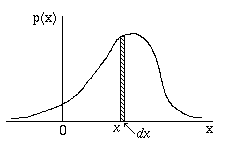 |
Grafico 2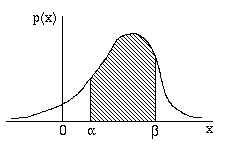 |
Vediamo ora come come trovare la funzione di distribuzione cumulativa partendo dalla densità di probabilità. Per definizione abbiamo:
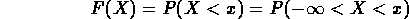
Osservando come abbiamo ricavato la probabilità che una variabile aleatoria appartenga ad un certo intervallo o attraverso il processo inverso di derivazione della densità di probabilità, otteniamo:

Geometricamente F(x) non è altro che che l'area compresa tra la curva di densità e l'asse delle ascisse e situata a sinistra del punto x (zona tratteggiata).