Nel momento in cui si parla di distribuzioni di probabilità
per variabili aleatorie continue, bisogna prestare un attimo di
attenzione ad un'importante questione. Attribuendo alla variabile
aleatoria la potenza del continuo, accade che in un qualsiasi
intervallo finito cadano un'infinità di valori della variabile
stessa: di conseguenza non si può pensare di attribuire a
ciascuno di essi un valore finito della probabilità.
Per questo motivo introduciamo alcuni concetti fondamentali che
in seguito ci saranno molto utili per lo studio delle
distribuzioni di variabili continue.
La funzione di distribuzione cumulativa per una variabile aleatoria continua X è definita come la probabilità che la variabile X assuma un qualsiasi valore minore di un valore x:
La funzione di distribuzione cumulativa è una caratteristica
di una variabile aleatoria. Essa esiste per tutte le variabili
aletorie, siano esse discrete o continue.
Vediamone ora alcune proprietà fondamentali:
> 
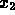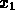si ha 
.
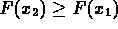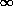la funzione di
distribuzione tende a zero: 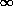) = 0
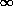la funzione di distribuzione
tende a uno: 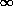) = 1
Senza dare una dimostrazione rigorosa di queste proprietà
vediamo come esse siano di facile comprensione attraverso un
esempio: esempio che, per facilitare la comprensione, viene
presentato inizialmente per variabili discrete.
Supponiamo di avere una variabile aleatoria discreta che può
assumere solo cinque valori: le probabilità di ottenere i
singoli valori sono raccolte nella tabella seguente.
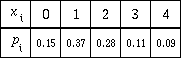
Andiamo ora a "costruire" la funzione di distribuzione cumulativa, tenendo presente che
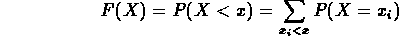
dove la disuguaglianza 
<x sotto il segno di
sommatoria significa che questa è estesa a tutti gli inferiori ad x.
Percui abbiamo
Il grafico di tale funzione è dunque il seguente:
graf.gif)
La funzione di distribuzione cumulativa di una variabile
discreta qualsiasi è sempre una funzione discontinua a gradini i
cui salti sono localizzati nei punti corrispondenti ai valori
possibili di questa variabile e sono uguali alle probabilità di
questi valori. La somma di tutti i salti della funzione, in
accordo con il terzo assioma della
probabilità, è pari a uno.
A mano a mano che aumenta il numero di valori possibili della
variabile aleatoria e diminuiscono gli intervalli tra di essi, il
numero di salti diventa sempre più grande e i salti stessi più
piccoli. La curva inizialmente a gradini della funzione si
avvicina così a una funzione continua, caratteristica delle
variabili aleatorie continue.
Definita la funzione di distribuzione cumulativa, vediamo cosa
succede se consideriamo la probabilità che la variabile assuma
un qualsiasi valore entro un intervallo di estremi 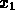e 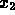: avremo allora
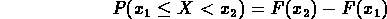
Infatti, l'appartenenza della variabile X
all'intervallo di estremi 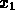e 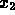equivale al verificarsi della
disuguaglianza
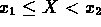
Esprimendo la probabilità di questo evento attraverso i seguenti tre eventi
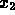
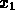
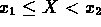
abbiamo che l'evento A si può esprimere come la somma
degli altri due, cioè A = B + C.
Per il teorema di addizione
delle probabilità abbiamo
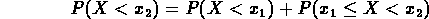
da cui ricaviamo la formula che avevamo introdotto
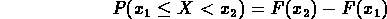
Operando un processo al limite percui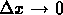 
, il rapporto tra la differenza della
funzione di distribuzione cumulativa e l'intervallo stesso è la
derivata
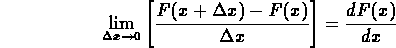
Si definisce la densità di probabilità o funzione di distribuzione:
La funzione p(x) caratterizza la densità di distribuzione dei valori della variabile aleatoria in un dato punto x: la densità di probabilità è una delle forme per esprimere la legge di distribuzione delle variabili aleatorie.
La condizione di normalizzazione non è altro che la
generalizzazione al caso continuo del terzo assioma della probabilità.
Analogamente al caso discreto, nel caso continuo deve valere la
seguente
che deriva dal fatto che F(+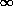)=1.
Note
Distribuzioni
discrete
Principali
distribuzioni continue