Una tipica situazione nella quale entra in gioco la
distribuzione di Poisson è lo studio di un processo di
decadimento radioattivo.
In questa circostanza, il numero di prove è costituito dal
numero di nuclei che potenzialmente possono decadere ed è molto
grande (per una mole di materiale radioattivo il numero di nuclei
è dell'ordine di 1023), mentre la probabilità di
"successo" (decadimento) per ogni nucleo è molto
piccola.
Si suppone che la probabilità p di decadimento sia
costante e inoltre, altra caratteristica tipica dei cosiddetti
processi di Poisson, che la probabilità di successo in un
intervallo di tempo [t, t+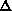
t]
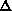sia proporzionale, in prima approssimazione, a t.
Vediamo ora la forma matematica di tale distribuzione. Una variabile aleatorie si distribusce in modo poissoniano se la probabilità di ottenere m successi è data da:
dove la grandezza a è detta parametro della
legge di Poisson e rappresenta la frequenza media di
accadimento dell'evento osservato.
Ad esempio, la probabilità di ottenere due successi è data da e-aa2/2!,
quella di ottenerne tre è e-aa3/3!
e via dicendo
Il valor medio della distribuzione è
mentre la deviazione standard è
Distribuzioni discrete
Esempi
Simulazione