Prima Legge di Fick: punto di vista
cinetico
Analisi Quantitativa
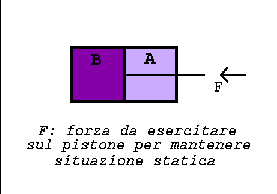
Consideriamo un cilindro riempito con due soluzioni della stessa
sostanza, posto
in un termostato alla temperatura costante T.
Un pistone permeabile alle molecole del solvente ma non a quelle
del soluto divide il cilindro in due parti, contenenti le due
soluzioni, A e B. La soluzione A
e` meno concentrata della B.
Il coefficiente di diffusione D da` il numero delle moli che si diffondono nell'unita` di tempo attraverso una sezione di area data per una caduta di concentrazione data.
Il moto delle singole particelle e` soggetto alle leggi fondamentali della meccanica del punto materiale, ma non manifesta nessuna direzione preferenziale.
Meta` delle molecole aderenti sui due lati dello strato considerato si muove verso sinistra, la restante meta` verso destra. Siccome il loro numero e`, come premessa, maggiore a sinistra che a destra, allora, attraverso il setto di separazione, si spostera` un maggior numero di particelle da sinistra verso destra cioe` verso il lato della soluzione diluita, rispetto alla direzione opposta. Questo processo termina soltanto quando la concentrazione diventa uguale in tutte le parti della soluzione in modo da avere una completa compensazione dei moti delle particelle nei due sensi attraverso il setto di separazione.
Conseguentemente, se nella camera A il soluto si trova in concentrazione maggiore che nella B, sul pistone si esercita una forza pari al prodotto della differenza tra le pressioni osmotiche nei due scomparti moltiplicata per la superficie S del pistone stesso. Ne segue che il pistone si muove verso destra, filtrando il solvente, fino a che la concentrazione di soluto nei due scomparti si eguaglia.
La forza che tende ad uguagliare la concentrazone nei due scomparti, e pertanto a provocare la diffusione del soluto fino ad occupare volumi tali da realizzare la predetta uguaglianza di concentrazione non e` altro che la pressione osmotica.
Il processo di diffusione puo` essere arrestato applicando dall'esterno
una forza F uguale e contraria a quella dovuta alla differenza di
pressione osmotica.
Supponiamo ora di togliere il setto di separazione della soluzione a concentrazione maggiore da quella a concentrazione minore.
Ricordando l'analogia che lega il moto delle particelle di soluto tra quelle di solvente e quello delle particelle che costituiscono un gas perfetto,
la forza che provoca il movimento diffusivo sara`:
A questo punto, nota la forza che provoca il movimento diffusivo, occorre determinare la resistenza che si oppone a tale movimento. Avendo adottato il modello di Einstein, la resistenza F' offerta al movimento delle molecole di soluto da parte di quelle del solvente e` data dalla relazione di Stokes
La F' agisce in opposizione a F, crescendo via via che F accelera le molecole, aumentandone la velocita`, sino ad una vlimite per la quale F ed F' risultano uguiali e contrarie. in un volume unitario di soluzione sono contenute nN molecole di soluto, dove N e` il numero di Avogadro ed n il numero di moli, dunque la forza F' (che agisce su una molecola), prima di essere eguagliata a F deve essere moltiplicata per il numero di molecole.
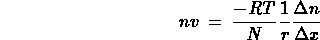(*)confrontando la (*) con la prima legge di Fick si osserva immediatamente che, a meno di un volume e di una mole, J = nv e dc/dx = dn/dx. Risulta quindi, ricordando la relazione di Stokes :
La teoria conduce quindi ad una precisa espressione per prevedere il valore del coefficiente di diffusione in funzione solamente della temperatura, della viscosita` del solvente e del raggio della molecola sferica del soluto.
La stessa relazione consente di determinare le dimensioni geometriche delle molecole del soluto , una volta che si sia determinato, con i metodi descritti nella sezione dedicata all'analisi macroscopica, il suo coefficiente di diffusione.
La permeazione attraverso le membrane
Ritorna al modello di Einstein
Indice
Animazione
Note