THE OSMOTIC PRESSURE: IT'S INTERPRETATION WITH EINSTEIN'S MODEL

First Fick's law: kinetic point of view
Quantitative Analysis

FIRST FICK'S LAW: KINETIC POINT OF VIEW

Let's consider a cylinder filled with two solution of the same substance. Put it in a thermostate at constant temperature T.
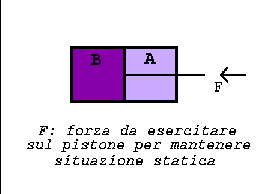
A piston which is permeable only to solvet molecules but not to that of the solute divide the cylinder into two parts: A and B. In A there is the less concentrate solution, in B the more concentrate.

Now let's try to understand the first Fick's law (italian) in the kinetic meaning.

The diffusion coefficient D gives the numbers of diffunding moles in a time unit unit of time, per a given area and per a given concentration decrease.

The motion of of a sinle particle do not obey to any rule and do not have a favourite direction.

Among the molecules in the two sides of the considered layer, half moves to the right and half to the left. As assumed, their number is bigger to the left than to the right, so a bigger number of them will move to right, the side of the more diluite solution, than to the other side. This process ends only when the concentration is equal everywhere inside the recipient: at that time all the movements compensate each other.

In B the solute has an higher concentration than in A: the force exerted on the piston is equal to the osmotic pressure difference times the area of the piston. So the partially permeable piston moves to the right filtering the solvent, till the solute concentration in the two chambers is equal.

Animation

The force which tends to equalize the concentration, in the two sections and therefore to make the solute diffuse, is due to the osmotic pressure.

The diffusion process can be stopped by applying from the exterior a force F equal and contrary to the force generated by the osmotic pressure difference.

        Animation

QUANTITATIVE ANALYSIS

Let now deffund the solute in a cylinder with no pistons, where concentration be bigger to the left than to the right.

The force which provoke the deffundent movement will be (italian)

In a unit of volume there are nN molecules of solute, where N is the Avogadro number, n the number of moles. The force k acting on these molecules will give them a velocity nN times lower. The force will be:

          (*)

With theorical arguments we arrive to an expression with which we can express the value of the diffusion coefficient vs temperature,viscosity, solvent and molecular radius of the solute.

The same relation permits to determine geometrical dimensions of the solute (italian) once determined the diffusion coefficient.

Back to the Einstein's model

Notes

Index