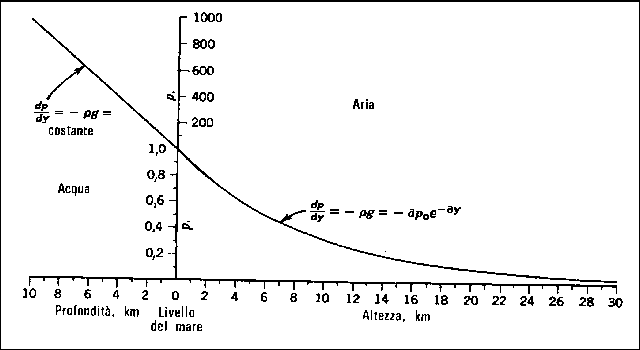
DIMINUZIONE ESPONENZIALE DELLA PRESSIONE ATMOSFERICA
La diminuzione della pressione con l'altitudine non è in realtà
così semplice come è stata esposta. Nel descrivere l'andamento
esponeziale delle variazioni di pressione nell'atmosfera
abbiamo supposto la temperatura dell'aria costante a 0°C,
cosa che non è.
Le variazioni di temperatura della superficie terrestre determinano
riscaldamenti e raffreddamenti dell'aria e di conseguenza diminuzioni e
aumenti di densità che si traducono in variazioni di pressione. In
uno stesso luogo si potranno verificare quindi variazioni di pressione
giornaliere o diurne, stagionali o irregolari.
Un esempio di variazione stagionale, per chiarire le idee, è la
formazione di una zona di alta pressione sull'Asia centrale in inverno,
sostituita da una zona di bassa pressione in estate, quando la temperatura
aumenta considerevolmente sul continente. Le variazioni irregolari sono
in relazione al carattere del tempo: la pressione diminuisce all'
avvicinarsi delle perturbazioni atmosferiche e aumenta nuovamente dopo il
loro passaggio.
In generale quindi la pressione atmosferica può variare da un luogo
all'altro o anche in uno stesso luogo per varie ragioni di ordine
metereologico. La pressione effettiva misurata in un dato luogo e ad una
data quota è quindi il risultato dei fattori fin qui
approssimativamente accennati.
Per il calcolo delle differenze di pressione dovute all'altitudine,
possiamo spiegare l'andamento da un punto di vista matematicamente più
formale assumendo che la densità
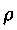 dell'aria sia proporzionale alla pressione (cosa che sarebbe esattamente
vera se la temperatura dell'aria fosse costante ad ogni quota).
Supponedo che anche la variazione del modulo dell'accelerazione
gravitazionale g sia trascurabile con la quota, potremo scrivere
l'equazione dell'equilibrio di un volume cilindrico infinitesimo di
area di base dA ed altezza dy:
dell'aria sia proporzionale alla pressione (cosa che sarebbe esattamente
vera se la temperatura dell'aria fosse costante ad ogni quota).
Supponedo che anche la variazione del modulo dell'accelerazione
gravitazionale g sia trascurabile con la quota, potremo scrivere
l'equazione dell'equilibrio di un volume cilindrico infinitesimo di
area di base dA ed altezza dy:
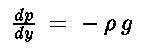
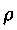 è proporzionale alla pressione si avrà:
è proporzionale alla pressione si avrà:
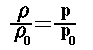
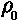 e p0 sono valori noti di densità e pressione a
livello del mare.
e p0 sono valori noti di densità e pressione a
livello del mare.
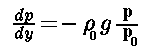
![dp/p= -[g*ro(0)/p(0)]*dy](/mflu/imgs/formule/app53.gif)
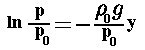
![p=p(0)* exp[- g*(ro(0)/p(0)) *y]](/mflu/imgs/formule/app55.gif)
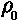 =
1,20 kg/m³ ( a 20°C ) e p0=1,01 ·
105 Pa, si può scrivere
=
1,20 kg/m³ ( a 20°C ) e p0=1,01 ·
105 Pa, si può scrivere
![p=p(0)* exp[-a*y]](/mflu/imgs/formule/app56.gif)
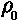 /
p0= 0,116 km-1.
/
p0= 0,116 km-1.