Conseguenza della
legge di Stevino ( vedi
anche il
paradosso idrostatico ) è che
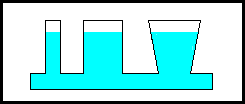
in un sistema di vasi comunicanti il fluido contenuto raggiunge la
stessa quota indipendentemente dalla forma dei recipienti.
Potendo scrivere la legge di Stevino nella forma
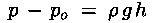
,
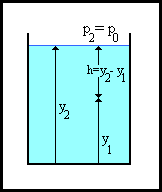
cambiando variabili come in figura la formula precedente può
essere riscritta come:
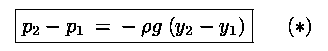
dove
p1,
y1 e
p2,
y2 sono rispettivamente
pressione e quota dei punti 1 e 2 dal livello di riferimento che questa
volta è stato preso sul fondo del recipiente contenente il fluido.
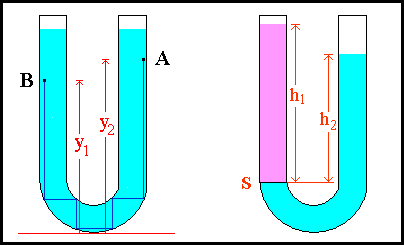
Da ciò segue che la quota raggiunta da un fluido nei due
bracci di un tubo ad U è la stessa.
Anche in questo caso la differenza di pressione tra due punti qualsiasi
si calcola attraverso la formula (*), in quanto per la legge di Stevino
si ha differenza di pressione solo in corrispondenza di variazioni di
quota: congiungendo i due punti A e B con tratti orizzontali e verticali
si hanno variazioni di P solo nei segmenti verticali.
Quindi la differenza di pressione
pB - pA è la somma algebrica delle
differenze sui segmenti verticali da A a B, cioè
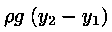
Se il tubo è riempito con liquidi non miscibili di densità
diverse
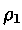
e

, le altezze
raggiunte dal fluido nei due rami saranno diverse:
h1
e
h2. Sulla superficie S di separazione tra i due
liquidi agiranno rispettivamente verso il basso e verso l'alto le
pressioni idrostatiche delle colonne
h1 e
h2. In condizioni di equilibrio le due pressioni si
bilanceranno:
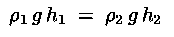
da cui:
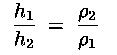
Pertanto due liquidi non miscibili in vasi comunicanti raggiungono
altezze inversamente proporzionali alle proprie densità.
Notiamo che possiamo vedere il principio dei vasi comunicanti nella
forma sopra enunciata come caso particolare di questa ultima formula:
se il liquido contenuto è uno solo
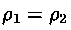
e quindi
h1 =
h2,
ovvero l'altezza raggiunta nei due bracci del tubo ad U è la stessa.
 Quesito
Quesito
 Applicazioni
Applicazioni
 Variazioni di pressione nei fluidi >
Variazioni di presione nei gas
Variazioni di pressione nei fluidi >
Variazioni di presione nei gas
 Variazioni di pressione nei fluidi <
Variazioni di presione nei liquidi < Il paradosso idrostatico
Variazioni di pressione nei fluidi <
Variazioni di presione nei liquidi < Il paradosso idrostatico
 Indice
Indice
Copyright © I.S.H.T.A.R. - March, 1999

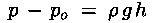 ,
,

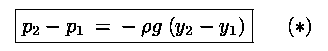
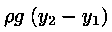

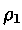 e
e
 , le altezze
raggiunte dal fluido nei due rami saranno diverse: h1
e h2. Sulla superficie S di separazione tra i due
liquidi agiranno rispettivamente verso il basso e verso l'alto le
pressioni idrostatiche delle colonne h1 e
h2. In condizioni di equilibrio le due pressioni si
bilanceranno:
, le altezze
raggiunte dal fluido nei due rami saranno diverse: h1
e h2. Sulla superficie S di separazione tra i due
liquidi agiranno rispettivamente verso il basso e verso l'alto le
pressioni idrostatiche delle colonne h1 e
h2. In condizioni di equilibrio le due pressioni si
bilanceranno:
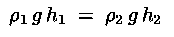
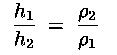
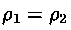 e quindi h1 = h2,
ovvero l'altezza raggiunta nei due bracci del tubo ad U è la stessa.
e quindi h1 = h2,
ovvero l'altezza raggiunta nei due bracci del tubo ad U è la stessa.
 Quesito
Quesito
 Applicazioni
Applicazioni