IL PARADOSSO IDROSTATICO

Una conseguenza della legge di Stevino
è che la pressione dipende solo dalla profondità alla quale
essa viene misurata e non dalla forma del recipiente che contiene il
fluido.
In tubi stretti ma sufficientemente alti è possibile produrre
pressioni notevoli anche con una piccola quantità di liquido se
l'altezza della colonna liqida è molto elevata. Un esempio di
ciò è la "botte di Pascal".
Il valore della pressione in un punto all'interno di un liquido
contenuto in un recipiente non dipende dalla forma di quest'ultimo.
Ciò si dimostra considerando il fatto che le pareti del
recipiente si deformano finché la loro forza elastica non fa
equilibrio alla pressione del fluido e quindi, agli effetti della
pressione, equivalgono alla presenza di altre parti di liquido.
Consideriamo i tre recipienti:
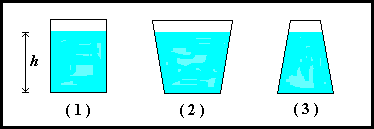
aventi ugual base e riempiti con uno stesso liquido fino ad una altezza
h. La pressione sul fondo di ogni recipiente dovuta al peso del
liquido, secondo la legge di Stevino, assume lo stesso valore
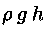 nei tre vasi.
nei tre vasi.
La forza F che agisce sul fondo è:
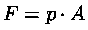
quindi

ovvero la forza è uguale al peso del liquido di volume
V = A·h, cioè il peso del liquido contenuto
nel vaso (1).
Il paradosso idrostatico consiste proprio in questo:
pur essendo il peso del liquido contenuto nei vari recipienti diverso a
seconda dei casi, la forza esercitata sul fondo ( nelle condizioni sopra
indicate ) è uguale per tutti e tre i casi e pari al peso del
liquido contenuto nel recipiente (1).

Per il recipiente (2) il peso del liquido contenuto è maggiore del
peso del liquido in (1) e, per quanto detto sopra, maggiore della forza
esercitata sul fondo. Il paradosso in questo caso si spiega con il
fatto che parte del peso del liquido contenuto è sostenuto dalla
forza normale R, avente componente P' verso l'alto,
esercitata dalle pareti del recipiente stesso.
In effetti la porzione di liquido ombreggiata
è sostenuta dai lati del recipiente.
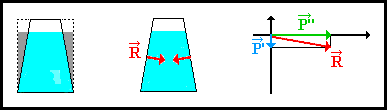
Per lo stesso principio nel caso del recipiente (3) la forza di reazione
delle pareti del recipiente avrà una componente P' verso il basso
che andrà a sommarsi al peso del liquido a quella quota e darà
comunque come risultato una forza F di intensità equivalente al
peso del liquido contenuto in (1) ( in questo caso il peso del liquido
contenuto in (3) è minore di quello contenuto in (1) ).
 Esempi
Esempi
 Variazioni di pressione nei fluidi >
Variazioni di presione nei liquidi > Principio dei vasi comunicanti
Variazioni di pressione nei fluidi >
Variazioni di presione nei liquidi > Principio dei vasi comunicanti
 Variazioni di pressione nei fluidi <
Variazioni di presione nei liquidi < Il Principio di Pascal
Variazioni di pressione nei fluidi <
Variazioni di presione nei liquidi < Il Principio di Pascal
 Indice
Indice
Copyright © I.S.H.T.A.R. - March, 1999
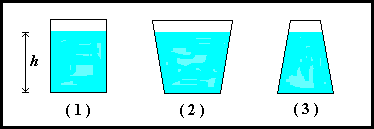
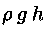 nei tre vasi.
nei tre vasi.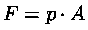



 Esempi
Esempi