

Supponiamo di aver realizzato N misure della stessa
grandezza e che i singoli valori ottenuti  si siano distribuiti normalmente attorno al
valor medio X con larghezza
si siano distribuiti normalmente attorno al
valor medio X con larghezza  :
vogliamo a questo punto conoscere l'affidabilità della
"media delle N misure".
:
vogliamo a questo punto conoscere l'affidabilità della
"media delle N misure".
Per fare ciò immaginiamo di ripetere il nostro gruppo di N
misure molte volte e per ciascuna di esse andiamo a calcolare la
media. Quello che vogliamo fare è trovare la distribuzione di
queste determinazioni della media delle N misure.
Calcoliamo, in ciascuna sessione di misure, la media
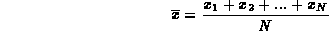
Essendo il valore medio di ciascuna delle  pari a X, il valore di
pari a X, il valore di  risulta
risulta
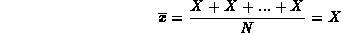
E fin qui tutto bene, nel senso che dopo aver effettuato
molte determinazioni della media  di N misure, i nostri molti risultati per
di N misure, i nostri molti risultati per  si saranno distribuiti normalmente
attorno al valore vero X.
si saranno distribuiti normalmente
attorno al valore vero X.
L'unico problema che ci resta da risolvere (ed è quello che ci
interessa) è quello di trovare la larghezza della nostra
distribuzione di risultati. Essendo fondamentalmente la media
funzione di tutte le N misure  , la la
formula generale per la propagazione delle incertezze per
funzioni di più variabili ci da
, la la
formula generale per la propagazione delle incertezze per
funzioni di più variabili ci da
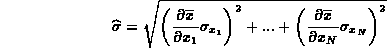
Dal momento che le misure  sono tutte misure della stessa grandezza,
le loro larghezze sono tutte le stesse ed uguali a
sono tutte misure della stessa grandezza,
le loro larghezze sono tutte le stesse ed uguali a  ; inoltre tutte le derivate parziali
presenti nella formula sono uguali ad 1/N data la definizione
stessa di media scritta poc'anzi.
; inoltre tutte le derivate parziali
presenti nella formula sono uguali ad 1/N data la definizione
stessa di media scritta poc'anzi.
Allora abbiamo
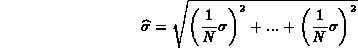
ossia otteniamo
