Introdurremo ora la formula generale per la propagazione
degli errori inerente a funzioni di più variabili: attraverso la
sua applicazione saremo in grado di risolvere problemi di
propagazione delle incertezze.
La necessità di introdurre una formula generale deriva dal fatto
che la semplice propagazione passo per passo può talvolta dar
luogo a degli errori di valutazione dell'incertezza nel risultato
finale: questo accade ad esempio quando in un quoziente la stessa
grandezza compare sia al denominatore che al numeratore. In
questo caso i due contributi dovuti alle incertezze dei due
fattori uguali potrebbero compensarsi parzialmente e attraverso
la formula della propagazione passo per passo rischieremmo di
dare una sovrastima dell'errore sul rapporto.
Vediamo come procedere partendo da un esempio:
Sfruttando il calcolo dell'incertezza per passi, si dovrebbero calcolare gli errori sulle due somme x + y e x + w e successivamente quello sul quoziente rischiando però di trascurare una eventuale interazione tra i due fattori. Se infatti la nostra stima di x fosse errata, ad esempio, in eccesso avremmo che sia il denominiatore che il numeratore risulterebbero sovrastimati, ma tale errore di valutazione verrebbe in parte celato se non totalmente cancellato dalla successiva operazione di divisione. Analogamente l'effetto di una eventuale sottostima di entrambe i fattori risulterebbe celato dal quoziente.
Consideriamo allora una funzione qualsiasi di due variabili del tipo
z = z (x , y)
Poichè le nostre migliori stime per x e y sono 
e 
ci aspettiamo che la migliore
valutazione per z sia
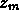= z
( , )
Per quanto riguarda il calcolo dell'incertezza su z dobbiamo ampliare il discorso già fatto nel caso di una variabile: dobbiamo cioè introdurre la seguente approssimazione per una funzione di due variabili
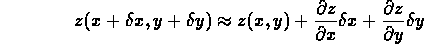
Tenendo presente che i valori probabili degli estremi per x
e y sono dati da 
e 
e che le derivate parziali in x
e y possono essere sia positive che negative, otteniamo
che i valori estremi di z sono dati da
Da questa ricaviamo subito che l'errore su z (x , y) è proprio
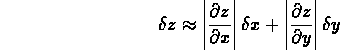
Se consideriamo la somma in quadratura possiamo rimpiazzare il risultato ottenuto con una stima più affinata: definiamo allora una regola generale per la propagazione degli errori in funzioni di più variabili.
, 
, ... ,
e tali valori vengano
utilizzati per calcolare la funzione z (x , y, ... ,w),
allora l'errore su z è dato da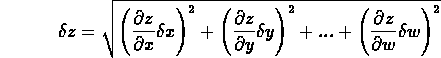 
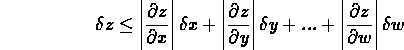
Da questa regola si possono facilmente ricavare tutte la altre già viste nei casi di operazioni più semplici, mentre l'uso diretto della formula può risultare un po' macchinoso: quando è possibile si preferisce procedere con il calcolo passo per passo ricordando però che nel caso in cui la stessa variabile compaia più volte nell'espressione questo metodo può portare a delle stime errate.
Regola
generale per la propagazione degli errori per funzioni di una
variabile
