DISTRIBUZIONI LIMITE

Si parla di distribuzioni limite nel momento in cui il numero di eventi considerati si avvicina all'infinito.
Con la dicitura "si avvicina all'infinito" si intende un numero di eventi, o realizzazioni di una variabile aleatoria, sufficientemente grande, ma anche qui la nostra definizione, di fatto, è ancora poco chiara.
Quello che si vuole dire, quando si parla di distribuzioni limite, è che dopo un certo numero di eventi, i risultati ottenuti si disporranno secondo una determinata distribuzione, mostreranno cioè, al passare delle prove, una detrminata distribuzione. Tale distribuzione diviene sempre più evidente all'aumentare degli eventi e, al limite per il numero di realizzazioni che tende all'infinito, la distribuzione assume un carattere continuo.

Vediamo di illustrare quanto detto con un esempio. Consideriamo i tre istogrammi sottostanti i quali mostrano le frazioni (f) di misure che cadono nei rispettivi intervalli (x=cm) nei casi in cui siano state effettuate 10, 100 e 1000 misure della stessa grandezza.

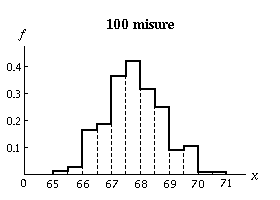
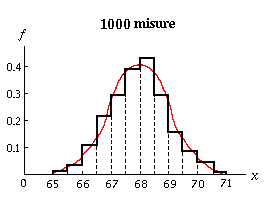
Si vede abbastanza bene che all'aumentare del numero di misure che effettuiamo la distribuzione dei dati ottenuti si avvicina ad una curva continua, definita. Quando ciò si verifica, la curva continua è detta distribuzione limite.
La distribuzione limite è una costruzione teorica, che non può mai essere misurata esattamente: più misure facciamo e più il nostro istogramma si avvicina alla distribuzione limite. Ma soltanto se noi fossimo in grado di effettuare un numero infinito di misure ed di utilizzare intervalli infinitamente stretti, allora otterremmo realmente la distribuzione limite stessa.