

Come nel caso delle differenze, la
trattazione della propagazione degli errori in un quoziente
risulta essere analoga al caso di un prodotto.
Consideriamo al solito la quantità z da calcolare come z
= x/y e i valori delle singole grandezze misurati
direttamente
valore misurato di x =  =
= 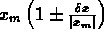
valore misurato di y =  =
= 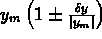
Allora il valore di z può essere espresso come

Se vogliamo trovare i valori dei probabili estremi entro i quali varia z dobbiamo guardare al secondo fattore dell'espressione: esso è massimo quando il numeratore assume il suo valore più grande e contemporaneamente il denominatore ha il suo valore più piccolo. in questo modo il valore più grande auspicabile per z è costituito da:
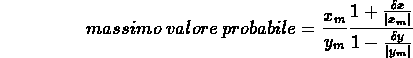
L'ultimo fattore di questa espressione si presenta nella forma
(1+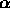 )/(1-
)/(1-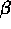 ) dove i termini
) dove i termini 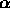 e
e 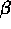 sono solitamente piccoli: questo
permette di eseguire alcune semplificazioni che ora andiamo a
effettuare.
sono solitamente piccoli: questo
permette di eseguire alcune semplificazioni che ora andiamo a
effettuare.
Come prima cosa, applicando il teorema binomiale
abbiamo che:

Da questa prima approssimazione ricaviamo
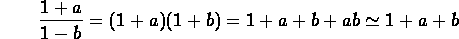
dove, nell'ultimo passaggio, abbiamo applicato un'ulteriore
approssimazione trascurando il prodotto dei due termini a
e b entrambe piccoli.
In definitiva, se osserviamo questo risultato e quello che
avevamo definito il valore massimo probabile di z vediamo
che quest'ultimo può essere riscritto in questa forma:

Un'analoga espressione con due segni meno si può ricavare per il valore minimo probabile: combinando le due espressioni possiamo concludere che il valore di z è dato da
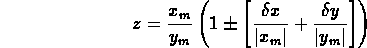
Se confrontiamo questa con la forma generale per z
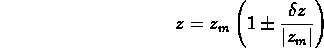
ritroviamo
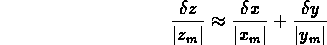
 Errori nei prodotti e quozienti
Errori nei prodotti e quozienti