Benchè alcuni integrali che si incontrano nello studio della distribuzione di Gauss siano risolvibili, nel momento in cui si voglia calcolare, attraverso l'integrazione della funzione densità di probabilità ci si trova di fronte ad un tipo di integrale non risolvibile analiticamente.
Esistono però delle tabelle dove sono raccolti i valori in più punti, calcolati attraverso metodi numerici.
In pratica, la probabilità che un variabile aleatoria cada in un intervallo centrato su m (valor medio) di larghezza è data da

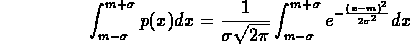
Più in generale potremmo calcolare la probabilità di ottenere una realizzazione della variabile in un intervallo centrato su m, ma questa volta largo t volte . In questo caso otteniamo:

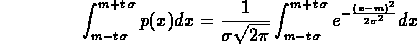
Come già detto questo integrale non è risolvibile analiticamente ma esistono delle tabelle che contengono la risoluzione numerica per diversi punti. In particolare a noi sarà sufficiente osservare il grafico seguente:

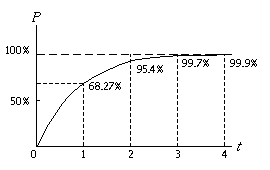
Questo grafico illustra la probabilità (P) che una misura cada entro t deviazioni standard rispetto al valor medio m.
Si vede che la probabilità che la variabile aleatoria (ad esempio il risultato di una misura) cada all'interno di una deviazione standard è di circa il 68%; la probabilità che cada all'interno di due deviazioni standard è 95.4%. Per 3 la probabilità è già del 99.7%, mentre per 4 deviazioni standard si ha una probabilità (99.9%).

Vediamo un esempio. Nel momento in cui trattiamo un campione di dati provenienti da una serie di misure e riteniamo che i dati si siano distribuiti secondo una normale, implicitamente operiamo alcune scelte. Se decidiamo infatti di associare alla nostra stima, calcolata come il valor medio della distribuzione, un'incertezza pari ad una deviazione standard significa che confidiamo che l'effetivo valore della grandezza misurata giaccia all'interno dell'intervallo, da noi definito, con una probabilità di circa il 68%.

La distribuzione di Gauss