

Calcoliamo i parametri fondamentali della legge normale e in particolare:
Nei paragrafi seguenti si farà un discreto uso del calcolo integrale, si consiglia perciò di visitare la seguente tabella prima di proseguire.
Utilizzando la definizione del momento iniziale di ordine 1 calcoliamo il valor medio della distribuzione di Gauss:
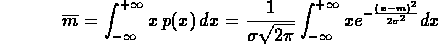
Operando il cambio di variabile:

ottenniamo
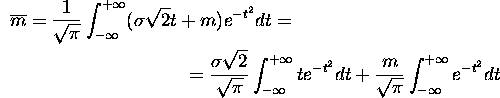
Nell'ultima espressione, il primo integrale è nullo, mentre il secondo è l'integrale di Eulero-Poisson:
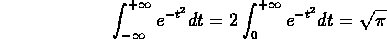
Di conseguenza otteniamo che  =m,
ossia il parametro m rappresenta proprio il valor medio
della distribuzione.
=m,
ossia il parametro m rappresenta proprio il valor medio
della distribuzione.
Per il calcolo della deviazione standard della normale sfruttiamo la definizione di varianza:
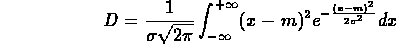
Effettuando il cambio di variabile

si ha
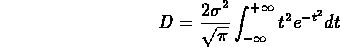
Integrando per parti, si giunge a:
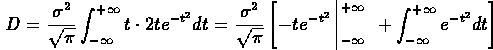
Il primo termine tra le parentesi quadre è nullo in quanto l'esponenziale negativo a più e meno infinito decresce molto più velocemente di quanto cresca qualsiasi potenza di t, mentre il secondo termine è l'integrale di Eulero-Poisson, per cui:

Quindi il parametro  nella
formula della distribuzione normale è non è altro che la
deviazione standard della distribuzione stessa.
nella
formula della distribuzione normale è non è altro che la
deviazione standard della distribuzione stessa.
Per quanto riguarda il parametro  si noti che, essendo l'ordinata massima inversamente proporzionale
a
si noti che, essendo l'ordinata massima inversamente proporzionale
a  , al crescere di
, al crescere di  il massimo della funzione cala e la
"campana" si allarga in quanto l'area delimitata dalla curva deve essere
sempre uguale all'unità: al contrario, al decrescere di
il massimo della funzione cala e la
"campana" si allarga in quanto l'area delimitata dalla curva deve essere
sempre uguale all'unità: al contrario, al decrescere di  la curva di distribuzione si allunga
verso l'alto restringendosi contemporaneamente ai lati,
diventanto cioè sempre più piccata sul valor medio.
la curva di distribuzione si allunga
verso l'alto restringendosi contemporaneamente ai lati,
diventanto cioè sempre più piccata sul valor medio.
Prima di passara al calcolo dei coefficienti di asimmetria e di appiattimento attraverso il
momento centrale di ordine 3 e quello di ordine 4, ricaviamo le
formule generali per imomenti centrali di qualsiasi ordine per la
distribuzione di Gauss.
Per definizione
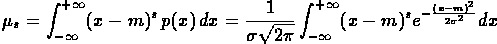
Dopo il cambio di variabile

si ha
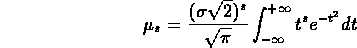
Integrando quest'ultima espressione per parti, si ottiene
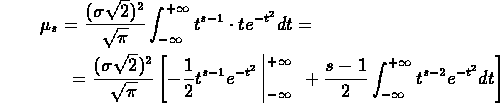
Tenendo conto che il primo termine entro le parentesi è nullo, rimane
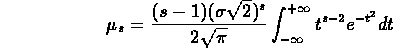
Se con lo stesso procedimento ricaviamo il momento centrale s-2-esimo otteniamo
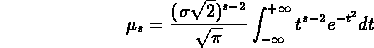
Confrontando i secondi termini delle ultime due espressioni,
si vede che esse differiscono solo per il fattore (s-1) 2: di conseguenza
possiamo affermare che vale
2: di conseguenza
possiamo affermare che vale

Quest'ultima è una formula ricorrente che permette di
esprimere i momenti di ordine superiore in termini di quelli
inferiori. Tenendo conto che il momento centrale di ordine 0 (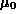 ) è uguale ad 1 e quello
di ordine 1 (
) è uguale ad 1 e quello
di ordine 1 (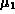 ) è
uguale a 0, si possono calcolare i momenti centrali di ordine
qualsiasi.
) è
uguale a 0, si possono calcolare i momenti centrali di ordine
qualsiasi.
In particolare, siccome 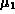 =0, segue che tutti i momenti di ordine
dispari della legge normale sono nulli, mentre per quanto rigurda
i momenti di ordine pari abbiamo
=0, segue che tutti i momenti di ordine
dispari della legge normale sono nulli, mentre per quanto rigurda
i momenti di ordine pari abbiamo
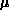 2=
2= 2
2 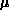 4=3
4=3 4
4 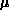 6=15
6=15 6
6
In generale la formula per il momento di ordine s qualunque è data da

dove, con il simbolo (s-1)!! si intende il prodotto di
tutti i numeri dispari tra 1 e s-1.
Poichè per la legge normale 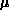 3=0, il suo coefficiente di
asimmetria è nullo:
3=0, il suo coefficiente di
asimmetria è nullo:

in accordo con la simmetria della distribuzione di Gauss.
Dall'espressione del momento di ordine quattro ricaviamo il
coefficiente di appiattimento

Ciò è del tutto naturale, in quanto il coefficiente di appiattimento caratterizza il grado di altezza raggiunto da una distribuzione effettiva in relazione alla distribuzione normale.