Il momento centrale di ordine s di una variabile aleatoria discreta si esprime attraverso la somma:
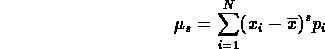
dove le 
rappresentano gli N valori possibili della variabile, 
rappresenta la media della variabile
e le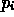 
sono le
probabilità che la variabile assuma i valori . Risulta abbastanza semplice vedere come
il momento centrale di ordine 1 sia nullo: infatti si ha
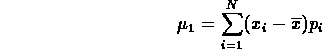
Essendo una costante, lo
posso portar fuori dalla sommatoria e ricordando la proprietà
del momento
iniziale di ordine 1 ho:
Passiamo ora a considerare il momento centrale di ordine 2
che riveste un ruolo molto importante nello studio delle
caratteristiche delle variabili aleatorie: data la sua importanza
lo indicheremo con la lettera D.
Il momento centrale di ordine 2, che ricordiamo essere
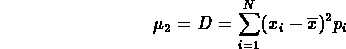
si chiama varianza della variabile aleatoria ed è una
caratteristica numerica inerente alla dispersione dei
valori della variabile attorno alla sua media.
Questa formula si può ulteriormente sviluppare come segue:
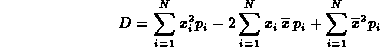
Tenendo presente che è una
costante, lo si può portare fuori dalle sommatorie, ottenendo
così
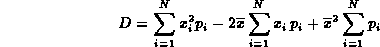
Il primo termine è il momento iniziale di ordine due, nel
secondo termine riconosciamo il momento iniziale di ordine uno
che sappiamo essere proprio e
infine il terzo termine presenta la somma delle probabilità 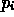che sappiamo essere, per
il terzo assioma della
probabilità, uguale ad uno. In definitiva otteniamo:
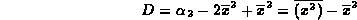
Notiamo che la varianza ha dimensione uguale al quadrato di
quella della variabile in esame: per questo motivo è talvolta
utile introdurre una seconda grandezza la cui dimensione coincide
con quella della variabile. A tal fine si estrae la radice
quadrata della varianza: la grandezza così ottenuta si dice scarto quadratico medio e si
indica con la lettera 
:
Generalmente per studiare le caratteristiche delle variabili aleatorie si considerano anche altri momenti centrali tra cui vale la pena ricordare i seguenti:
Caso di variabili continue
Definizioni