DISTRIBUZIONI CONTNINUE
- Distribuzione uniforme -
Proprietà della distribuzione uniforme
Determiniamo le caratteristiche numeriche fondamentali della
variabile aleatoria X soggetta alla legge di distribuzione
uniforme nell'intervallo (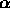
,
).
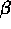Il valor medio, applicando la definizione di momento iniziale di ordine 1 nel
caso di variabili continue, vale
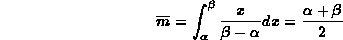
In virtù della simmetria della distribuzione il valore della
mediana coincide con
quello del valor medio. Si tenga inoltre presente che la
distribuzione uniforme non ha moda.
ora, attraverso il momento
centrale di ordine 2 nel caso continuo, calcoliamo la
varianza e da questa la deviazione standard:
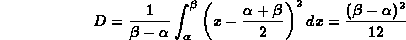
da cui la deviazione standard
Esempi
-
- Esempio 1. Un corpo viene pesato con una bilancia
di precisione avendo a disposizione solo pesi multipli di
1 g.; i risultati mostrano che il peso del corpo è
compreso tra k e k+1 grammi. Se si assume
che questo peso sia uguale a (k+1/2) grammi,
l'errore commesso (X) è, evidentamente, una
variabile aleatoria, distribuita con densità di
probabilità uniforme nell'intervallo (-1/2, 1/2) g.
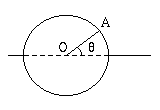
- Esempio 2. Una ruota simmetrica in rotazione si
arresta a causa dell'attrito. L'angolo formato da un
raggio mobile della ruota con un raggio fissato OA
dopo l'arresto della ruota è una variabile la cui
densità di distribuzione è uniforme in (0, 2
).
Distribuzioni continue
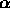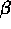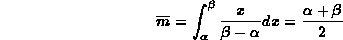
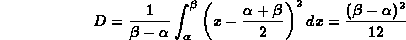
Indice
