Attraverso questo teorema calcoliamo la probabilità di più
eventi, sia che essi accadano insieme oppure in alternativa l'uno
all'altro. Consideriamo due eventi: se essi sono mutuamente
escludentesi allora la probabilità che accada o uno o l'altro è
data dal secondo assioma della
probabilità, mentre se l'accadere di uno non preclude la
possibilità che si presenti anche il secondo allora bisogna
ragionare in un altro modo.
Nel caso che due eventi non siano mutuamente escludentesi, il teorema di addizione delle probabilità afferma che
P(A
B) = P(A) + P(B) - P(A
B)
che equivale a
P(A+B) = P(A) + P(B) - P(A
B)
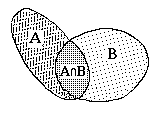La
dimostrazione del teorema si ricava osservando la figura accanto:
se i due insiemi rappresentano rispettivamente la probabilità di
successo dell'evento A e dell'evento B allora la probabilità che
si verifichi almeno uno dei due è uguale alla somma delle aree
dei due insiemi.
Però nel momento in cui si considera l'unione dei due insiemi
bisogna togliere la quantità relativa alla loro intersezione in
quanto viene cosiderata due volte: una volta per ciascun insieme.
Il teorema dell'addizione delle probabilità, come nel caso del prodotto, è facilmente estendibile a più di due eventi, sempre operando le stesse considerazioni che abbiamo fatto per i due eventi A e B.
Torna
alla pagina precedente