

Per prodotto delle probabilità, in generale di due eventi si
intende il verificarsi di entrambe simultaneamente. Ad
esempio, se l'evento A consiste nell'estrazione di un due da un
mazzo di carte e l'evento B nell'estrazione di una carta di
picche, allora l'evento C=A B consiste nell'apparizione di un due
di picche.
B consiste nell'apparizione di un due
di picche.
Il teorema si può quindi scrivere nella seguente forma:
P(A B) = P(A) + P(B)
- P(A
B) = P(A) + P(B)
- P(A B)
B)
che equivale a
P(A B) = P(A) +
P(B) - P(A+B)
B) = P(A) +
P(B) - P(A+B)
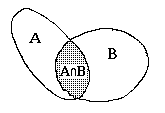 La
dimostrazione del teorema è failmente intuibile
dall'osservazione della figura a fianco dove la quantità P(A
La
dimostrazione del teorema è failmente intuibile
dall'osservazione della figura a fianco dove la quantità P(A B) corrisponde alla zona
ombreggiata della figura. Tale zona, nel caso della somma dei due
insiemi viene ricoperta due volte, quindi, togliendo la grandezza
P(A
B) corrisponde alla zona
ombreggiata della figura. Tale zona, nel caso della somma dei due
insiemi viene ricoperta due volte, quindi, togliendo la grandezza
P(A B) si eliminano le parti
non comuni dei due insiemi e in più si sottrae anche una volta
la superfice P(A
B) si eliminano le parti
non comuni dei due insiemi e in più si sottrae anche una volta
la superfice P(A B)
proprio come volevamo.
B)
proprio come volevamo.
Il teorema del prodotto delle probabilità, come nel caso dell'addizione è facilmente estendibile al caso di più variabili applicando le stesse considerazioni fatte nel caso di due variabili.
Esiste anche un'altra formulazione di questo teorema che va sotto il nome di teorema delle probabilità composte.