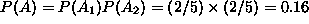TEOREMA DELLE
PROBABILITÀ COMPOSTE

Un altro modo per esprimere il teorema di moltiplicazione delle probabilità è rappresentato dal teorema delle probabilità composte. Tale teorema può essere enunciato nel modo seguente:

la probabilità del prodotto di due eventi è uguale al prodotto della probabilità di uno degli eventi per la probabilità condizionata dell'altro calcolata a condizione che il primo abbia luogo.

P(AB) = P(A) P(B|A) = P(B) P(A|B)

Si noti che se gli eventi A e B sono mutuamente escludentesi, la probabilità ccndizionata si annulla per definizione, mentre se gli eventi sono indipendenti si ha che P(B|A) = P(B) e analogamente P(A|B) = P(A): da quest'ultimo caso discende un corollario molto importante:

la probabilità del prodotto di due eventi indipendenti è uguale al prodotto delle probabilità di questi eventi.

P(AB) = P(A) P(B)

o in generale, per N eventi

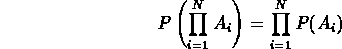
Un'urna contiene 2 palline bianche e 3 palline rosse. Si estraggono due palline dall'urna: trovare la probabilità che le due palline estratte siano entrambe bianche.

Denotiamo con A l'evento - apparizione di due palline bianche -. L'evento A è il prodotto di due eventi elementari

A =

dove rappresenta l'apparizione della pallina bianca alla prima estrazione e è la probabilità di ottenere la pallina bianca alla seconda estrazione.
In virtù del teorema delle probabilità composte

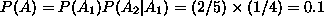
Consideriamo la stessa situazione in cui dopo la prima estrazione, la pallina estratta viene rimessa nell'urna (si parla allora di estrazione con reintroduzione): in questo caso gli eventi e sono indipendenti e per il corollario si ha:

Torna alla pagina precedente