

Oltre a queste esistono altri fattori tra cui il costo,
l'ingombro e il peso che contraddistinguono lo strumento: si noti
peraltro che le varie caratteristiche non sono indipendenti l'una
dall'altra, ma costituiscono il risultato di un compromesso che
si raggiunge all'atto della progettazione.
Come esempio si consideri il fatto che il costo di uno strumento
può salire notevolmente all'aumentare dell'intervallo di
funzionamento e non è detto che le due grandezze, costo e
intervallo di funzionamento, siano correlate linearmente: anzi
molto spesso ad un piccolo ampliamento delle caratteristiche
(precisione, intervallo di funzionamento e così via)
corrisponde, in proporzione, un aumento dei costi ben superiore
ai miglioramenti apportati. 
Con il termine ripetibilità si intende la capacità dello
strumento di fornire misure uguali della stessa grandezza entro
la sua risoluzione, anche in
condizioni di lavoro difficili o variabili (vibrazioni, sbalzi di
temperatura, ...).
In pratica lo strumento deve risultare ben isolato rispetto agli
effetti dell'ambiente esterno, escluso ovviamente l'effetto
dovuto alla grandezza in esame.
La ripetibilità implica anche una buona affidabilità intesa come robustezza di funzionamento nel tempo: questa peculiarità viene espressa come vita media o come tempo medio statisticamente prevedibile fra due guasti successivi in condizioni normali di utilizzo.
La prontezza è una caratteristica dello strumento legata al
tempo necessario affinchè questo risponda ad una variazione
della grandezza in esame. Per alcuni, quanto minore è questo
tempo, detto tempo caratteristico, tanto maggiore è la
prontezza, mentre per altri la prontezza è rappresentata dal
tempo impegato dallo strumento per dare la risposta, cioè il
risultato.
In generale la prontezza rappresenta la rapidità con cui è
lo strumento è in grado di fornire il risultato di una misura.
Per chiarire quanto detto finora vediamo un esempio:
consideriamo un termometro a mercurio, quello che si può trovare
in un comune laboratorio, che sia inizialmente alla temperatura
ambiente di 20oC.
Se ora lo immergiamo in un bagno di liquido alla temperatura di
120oC osserviamo che il mercurio comincia a salire
lungo la scala prima velocemente poi più lentamente fino ad
arrivare al valore di temperatura corrispondente:
approssimativamente il tempo impiegato affinchè il mercurio
raggiunga la posizione relativa alla temperatura misurata è
dell'ordine di qualche decina di secondi (diciamo 40).
Questo intervallo di tempo ci da un'indicazione sulla prontezza
dello strumento: in particolare se andiamo ad osservare
l'andamento della temperatura misurata graficata rispetto al
tempo, il fenomeno descritto appare ancora più chiaro.

C'è anche chi definisce la prontezza come il tempo impiegato
dall'indice dello struento (nel nostro caso il livello della
colonnina di mercurio) ad effettuare il 63.2 % dell'escursione
che esso deve compiere, partendo dalla posizione iniziale di
riposo fino a raggiungere il valore effettivo della grandezza:
tale tempo è definito come coefficiente di ritardo.
Attraverso questa definizione si potrebbe avere un coefficiente
di ritardo variabile con il valore della grandezza applicata: per
ovviare a questo inconveniente occorre fissare un valore di
riferimento della grandezza, le modalità d'uso e tutte le altre
caratteristiche strumentali in modo tale che la prontezza così
definita rispecchi un'effettiva caratteristica dell'apparecchio.
La sensibilità di uno strumento è costituita dalla
più piccola grandezza in grado di generare uno spostamento
apprezzabile rispetto all'inizio della scala dello strumento.
Così definita, la sensibilità determina il limite inferiore del
campo di misura dello strumento, mentre il limite superiore è
dato dal fondo scala: i due
determinano insieme l'intervallo
di funzionamento.
Esiste anche una definizione più raffinata di quella presentata, anche se concettualmente sono del tutto equivalenti.
La risoluzione di uno strumento rappresenta la minima
variazione apprezzabile della grandezza in esame attraverso tutto
il campo di misura: essa rappresenta il valore dell'ultima cifra
significativa ottenibile.
Percui se la scala dello strumento parte da zero ed è lineare la
risoluzione è costante lungo tutto il campo di misura e risulta
numericamente uguale alla sensibilità.
Si osservi che non sempre sensibilità e risoluzione coincidono: la loro differenza risiede nella definizione delle due grandezze. Infatti la sensibilità è relativa all'inizio del campo di misura, mentre la risoluzione è considerata sull'intero campo di misura dello strumento.
Il fondo scala rappresenta il limite superiore del campo di misura e prende anche il nome di portata dello strumento: insieme alla sensibilità ne delimita l'intervallo di funzionamento.
Come abbiamo già detto, ad ogni misura è associata
inevitabilmente una incertezza. Evidentemente più piccola è
l'incertezza associata alla misura, migliore sarà la misura.
Ma cosa significa "più piccola"?
Vediamo di chiarire questo punto. Quando noi forniamo un
risultato, lo dobbiamo sempre corredare, oltre che del valore
della misura, anche dell'errore associato: tale errore è detto errore
assoluto e rappresenta l'intervallo di indeterminazione entro
il quale si suppone che il risultato sia compreso.
Se ora cosideriamo il rapporto tra l'errore assoluto e il
risultato stesso otteniamo una grandezza adimensionale (un
numero, privo cioè di unità di misura), molto utile
nell'analisi degli errori, che prende il nome di precisione
o errore
relativo.
A questo punto appare evidente che la misura con l'errore
relativo minore è quella più precisa: si noti bene che si è
parlato di errore relativo e non assoluto. Infatti si consideri
il seguente esempio.
Siano date due misure nel modo seguente
A=(10 ± 1) Kg
B=(100 ± 1) Kg
Entrambe hanno lo stesso errore assoluto (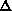 A=
A=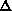 B=1
Kg), mentre hanno differenti errori relativi.
B=1
Kg), mentre hanno differenti errori relativi.
Ora, mentre nella prima misura abbiamo un errore di una unità su
dieci, nella seconda abbiamo un errore di una sola unità su
cento: si è allora soliti dire che la prima è una misura precisa
al 10%, mentre la seconda precisa al 1%.
Precisioni di questo ordine di grandezza sono molto simili a quelle che si possono ottenere in un laboratorio di fisica o di chimica: si tenga però conto che i laboratori di ricerca le precisioni raggiunte sono di parecchi ordini di grandezza superiori. Per questo si è soliti usare la notazione scientifica, onde evitare la scomodità di espressioni con troppi zeri.