DISTRIBUZIONI CONTINUE
- Distribuzione uniforme -

ProprietÓ della distribuzione uniforme
Le caratteristiche numeriche fondamentali di una variabile
aleatoria X soggetta alla legge di distribuzione uniforme
nell'intervallo (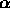 ,
,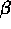 )sono le seguenti.
)sono le seguenti.
Il valor medio vale

In virt¨ della simmetria della distribuzione il valore della
mediana coincide con
quello del valor medio. Si tenga inoltre presente che la
distribuzione uniforme non ha moda.
La deviazione standard Ŕ pari a:

Esempi
-
- Esempio 1. Un corpo viene pesato con una bilancia
di precisione avendo a disposizione solo pesi multipli di
1 g.; i risultati mostrano che il peso del corpo Ŕ
compreso tra k e k+1 grammi. Se si assume
che questo peso sia uguale a (k+1/2) grammi,
l'errore commesso (X) Ŕ, evidentamente, una
variabile aleatoria, distribuita con densitÓ di
probabilitÓ uniforme nell'intervallo (-1/2, 1/2) g.
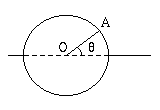
- Esempio 2. Una ruota simmetrica in rotazione si
arresta a causa dell'attrito. L'angolo formato da un
raggio mobile della ruota con un raggio fissato OA
dopo l'arresto della ruota Ŕ una variabile la cui
densitÓ di distribuzione Ŕ uniforme in (0, 2
 ).
).
Distribuzioni continue
 Indice
Indice


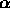 ,
,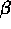 )sono le seguenti.
)sono le seguenti. ![]()

 ).
). 

 Indice
Indice